
分析 (1)写出任意一个三位阶梯数及其互逆数;
根据已知表示这个三位数和互逆数,并计算它们的差为:-198b,从而得出结论;
(2)先设未知数:设这个四位阶梯数的首位数字为a,差是b,这里b是连续加三次,所以不能大于3,还要注意a+b<9,且a、b为整数,所以要分情况讨论:
当b=0、±1、±2、±3时,代入四位数中依次计算,找出能补6整除的四位阶梯数.
解答 解:(1)三位阶梯数为:123,互逆数为:123和321,
根据题意得:百位数为a,则十位数字为:a+b,个位数字为:a+2b,
其互逆数的百位数为a+2b,则十位数字为:a+b,个位数字为:a,
则100a+10(a+b)+(a+2b)-[100(a+2b)+10(a+b)+a],
=100a+10a+10b+a+2b-100a-200b-10a-10b-a,
=-198b,
∴任意一个三位数与其互逆数的差能被198整除;
故答案为:123,123或321;
(2)设这个四位阶梯数的首位数字为a,差是b(1≤a≤9,|b|≤3,且a、b为整数),
①当b=0时,这四位数字都是a,则1000a+100a+10a+a=1111a,
当a=6时,这个四位阶梯数为6666,能被6整除;
②当b=1时,这四位数字分别是a、a+1、a+2、a+3,则1000a+100(a+1)+10(a+2)+a+3=1111a+123,
当a=3时,这个四位阶梯数为3456,能被6整除;
③当b=2时,这四位数字分别是a、a+2、a+4、a+6,则1000a+100(a+2)+10(a+4)+a+6=1111a+246,
此时没有能被6整除的四位阶梯数;
④当b=3时,这四位数字分别是a、a+3、a+6、a+9,则1000a+100(a+3)+10(a+6)+a+9=1111a+369,
此时没有能被6整除的四位阶梯数;
⑤当b=-1时,这四位数字分别是a、a-1、a-2、a-3,则1000a+100(a-1)+10(a-2)+a-3=1111a-123,
当a=3时,这个四位阶梯数为3210,能被6整除;
当a=9时,这个四位阶梯数为9876,能被6整除;
⑥当b=-2时,这四位数字分别是a、a-2、a-4、a-6,则1000a+100(a-2)+10(a-4)+a-6=1111a-246,
当a=6时,这个四位阶梯数为6420,能被6整除;
⑦当b=-3时,这四位数字分别是a、a-3、a-6、a-9,则1000a+100(a-3)+10(a-6)+a-9=1111a-369,
当a=9时,这个四位阶梯数为9630,能被6整除;
综上所述,符合条件的所有四位阶梯数分别是:6666、3456、3210、9876、6420、9630.
点评 本题考查了因式分解的应用、整式的加减,比较复杂,利用因式分解解决求值问题和证明问题;灵活利用整数的整除性.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
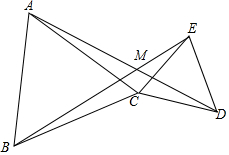 如图,两个等腰角形△CAB与△CED,其CA=CB,CE=CD,∠ACB=∠ECD=α,连接AD、CE.求证:
如图,两个等腰角形△CAB与△CED,其CA=CB,CE=CD,∠ACB=∠ECD=α,连接AD、CE.求证:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
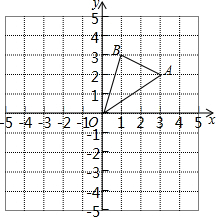 如图,△AOB的顶点均在格点上,每个小正方形的边长均为1个单位长度.
如图,△AOB的顶点均在格点上,每个小正方形的边长均为1个单位长度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
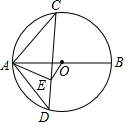 如图,AB是⊙O的直径,C是半圆的中点,连接CA,E是弦CD上一点,CE=CA,连接AD.
如图,AB是⊙O的直径,C是半圆的中点,连接CA,E是弦CD上一点,CE=CA,连接AD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,D是直径AB延长线上一点,C是圆O上一点且CO⊥AB,连接CB,DE与圆O相切于E,EF与AB相交于F.
如图,D是直径AB延长线上一点,C是圆O上一点且CO⊥AB,连接CB,DE与圆O相切于E,EF与AB相交于F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com