
分析 (1)函数图象经过原点,即函数解析式的常数项为0,构造方程即可求出实数k的值;
(2)函数y=x2-2kx+k2+k-2图象的顶点坐标为(k,k-2),根据第四象限点的坐标符号构造不等式,解得实数k的取值范围.
解答 解:(1)当k2+k-2=0
即k=-2,或k=1
函数y=x2-2kx+k2+k-2的图象经过原点
(2)函数y=x2-2kx+k2+k-2图象的顶点坐标为(k,k-2)
若函数图象的顶点在第四象限内时,
$\left\{\begin{array}{l}{k>0}\\{k-2<0}\end{array}\right.$
解得:0<k<2.
点评 本题考查的知识点是二次函数的性质,其中熟练掌握二次函数的图象和性质特别是对称轴方程顶点坐标及对称性是解答的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -2x6y16 | B. | -2x6y32 | C. | -2x3y8 | D. | -4x6y16 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
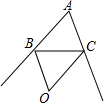 如图,在△ABC中,∠ABC和∠ACB的外角平分线交于点O,设∠A=m,则∠BOC=( )
如图,在△ABC中,∠ABC和∠ACB的外角平分线交于点O,设∠A=m,则∠BOC=( )| A. | 90°-m | B. | 90°-$\frac{m}{2}$ | C. | 180°-2m | D. | 180°-$\frac{m}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com