
分析 (1)展开后移项合并同类项后转化为一元一次方程求解即可;
(2)将代数式的前两项提取公因式后整体代入即可求解.
解答 解:(1)2x3-2x(x2-2x+6)=-4x(1-x)+16,
展开得:2x3-2x3+4x2-12x=-4x+4x2+16,
移项得:-12x+4x=16,
合并同类项得:-8x=16,
解得:x=-2;
(2)∵m2+m-1=0,
∴m2+m=1,
∴原式=m3+m2+m2+2014=m(m2+m)+m2+2014=m2+m+2014=1+2014=2015,
点评 本题考查了解一元一次方程、因式分解的应用、整式的混合运算等知识,考查知识比较多,但相对比较基础,难度不大.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 开口向下 | B. | 对称轴是直线x=-1 | ||
| C. | 顶点坐标是(1,2) | D. | 与x轴有两个交点 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
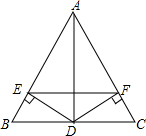 如图,△ABC是等边三角形,D是BC边的中点,过点D分别作AB、AC的垂线,垂足为E、F.
如图,△ABC是等边三角形,D是BC边的中点,过点D分别作AB、AC的垂线,垂足为E、F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com