
分析 (1)首先化简二次根式,计算乘方、开方,去掉绝对值符号,然后合并同类二次根式即可;
(2)首先计算乘方,然后进行乘法运算,最后合并同类项即可求解;
(3)首先计算乘方,然后进行乘法运算,最后合并同类项即可求解;
(4)首先对中括号内的式子进行化简,然后进行乘法运算即可;
(5)首先逆用积的乘方公式,然后进行加法运算即可;
(6)首先根据绝对值的性质去掉绝对值符号,然后合并同类二次根式即可.
解答 解:(1)原式=-$\frac{1}{2}$-(7-$\sqrt{3}$)+7×1+1=-$\frac{1}{2}$-7+$\sqrt{3}$+7+1=$\frac{1}{2}$+$\sqrt{3}$;
(2)原式=8a6•a3-64a9+81a4•a5=8a9-64a9+81a9=25a9;
(3)原式=-27a6b3c3•3a2b2•b2c2+9a2b4c2•a6b3c3=-81a8b7c5+9a8b7c5=-72a8b7c5;
(4)原式=[3ab-ab2-2ab+ab2]•(-2a2b3)=ab•(-2a2b3)=-2a3b4;
(5)原式=-8×[8×(-0.125)]2014+(-0.25×4)3=-8×1-1=-8-1=-9;
(6)原式=$\sqrt{2}$-1+$\sqrt{3}$-$\sqrt{2}$+$\sqrt{4}$-$\sqrt{3}$+…+$\sqrt{100}$-$\sqrt{99}$=$\sqrt{100}$-1=10-1=9.
点评 本题考查了二次根式的混合运算以及乘方的运算性质,二次根式运算时一般首先化简二次根式,然后进行计算.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | -2x6y16 | B. | -2x6y32 | C. | -2x3y8 | D. | -4x6y16 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
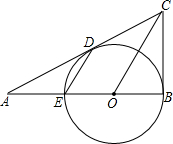 如图,已知,BE是⊙O的直径,BC切⊙O于B,弦DE∥OC,连接CD并延长交BE的延长线于点A.
如图,已知,BE是⊙O的直径,BC切⊙O于B,弦DE∥OC,连接CD并延长交BE的延长线于点A.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com