练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知抛物线经过A（0，﹣3）、B（2，﹣3）、C（4，5），判断点D（﹣2，5）是否在该抛物线上．你的 结论是：（填“是”或“否”）．

    【答案】是
    【解析】解：∵抛物线经过A（0，﹣3）、B（2，﹣3）， 而点A与点B关于直线x=1对称，
    ∴抛物线的对称轴为直线x=1，
    ∴点C（4，5）关于直线x=1的对称点D（﹣2，5）在抛物线上．
    故答案为：是．
    利用点A与点B的坐标特征得到抛物线的对称轴为直线x=1，然后根据抛物线的对称性可判断点C（4，5与点D（﹣2，5）是抛物线上的对称点．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】四边形ABCD中，AC⊥BD，顺次连接它的各边中点所得的四边形是_________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】解不等式组 ，并求它的整数解．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】用一个平面截去正方体的一个角，则截面不可能是（　　）

    A. 等腰直角三角形 B. 等腰三角形

    C. 锐角三角形 D. 等边三角形

    查看答案和解析>>

    科目：初中数学 来源： 题型：

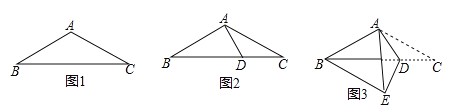
    【题目】如图1，在等腰三角形ABC中，AB=AC=4，BC=7．如图2，在底边BC上取一点D，连结AD，使得∠DAC=∠ACD．如图3，将△ACD沿着AD所在直线折叠，使得点C落在点E处，连结BE，得到四边形ABED．则BE的长是（ ）

    A．4 B． C． D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】代数式2x﹣4y﹣3中，y的系数是 ， 常数项是 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

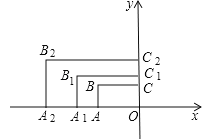
    【题目】如图，在平面直角坐标系中，矩形AOCB的两边OA、OC分别在x轴和y轴上，且OA=2，OC=1．在第二象限内，将矩形AOCB以原点O为位似中心放大为原来的倍，得到矩形A1OC1B1，再将矩形A1OC1B1以原点O为位似中心放大倍，得到矩形A2OC2B2…，以此类推，得到的矩形AnOCnBn的对角线交点的坐标为 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

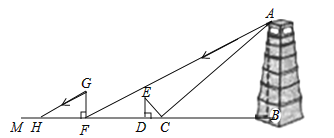
    【题目】某市为了打造森林城市，树立城市新地标，实现绿色、共享发展理念，在城南建起了“望月阁”及环阁公园．小亮、小芳等同学想用一些测量工具和所学的几何知识测量“望月阁”的高度，来检验自己掌握知识和运用知识的能力．他们经过观察发现，观测点与“望月阁”底部间的距离不易测得，因此经过研究需要两次测量，于是他们首先用平面镜进行测量．方法如下：如图，小芳在小亮和“望月阁”之间的直线BM上平放一平面镜，在镜面上做了一个标记，这个标记在直线BM上的对应位置为点C，镜子不动，小亮看着镜面上的标记，他来回走动，走到点D时，看到“望月阁”顶端点A在镜面中的像与镜面上的标记重合，这时，测得小亮眼睛与地面的高度ED=1.5米，CD=2米，然后，在阳光下，他们用测影长的方法进行了第二次测量，方法如下：如图，小亮从D点沿DM方向走了16米，到达“望月阁”影子的末端F点处，此时，测得小亮身高FG的影长FH=2.5米，FG=1.65米．

    如图，已知AB⊥BM，ED⊥BM，GF⊥BM，其中，测量时所使用的平面镜的厚度忽略不计，请你根据题中提供的相关信息，求出“望月阁”的高AB的长度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，学校准备新建一个长度为L的读书长廊，并准备用若干块带有花纹和没有花纹的两种规格大小相同的正方形地面砖搭配在一起，按图中所示的规律拼成图案铺满长廊，已知每个小正方形地面砖的边长均为0.3m．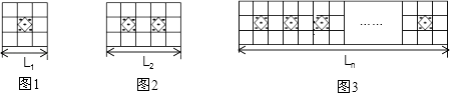

    （1）按图示规律，第一图案的长度L1=；第二个图案的长度L2=；
    （2）请用代数式表示带有花纹的地面砖块数n与走廊的长度Ln（m）之间的关系；
    （3）当走廊的长度L为30.3m时，请计算出所需带有花纹图案的瓷砖的块数．

    查看答案和解析>>

    同步练习册答案