
 如图,是抛物线y=ax2+bx+c(a≠0)图象的一部分,已知抛物线的对称轴是直线x=2,与x轴的一个交点是(-1,0),有下列结论:
如图,是抛物线y=ax2+bx+c(a≠0)图象的一部分,已知抛物线的对称轴是直线x=2,与x轴的一个交点是(-1,0),有下列结论:分析 根据抛物线的图象,数形结合,逐一解析判断,即可解决问题.
解答 解:∵抛物线开口向上,
∴a>0,b<0;由图象知c<0,
∴abc>0,故①错误;
∵抛物线的对称轴为x=2,
∴-$\frac{b}{2a}$=2,b=-4a,
∴4a+b=0,故②正确;
∵抛物线y=ax2+bx+c与x轴有两个交点,对称轴是x=2,与x轴的一个交点是(-1,0),
∴抛物线与x轴的另一个交点是(5,0);故③正确;
∵对称轴方程为 x=2,
∴(-2,y1)可得(6,y1)
∵(5,y2)在抛物线上,
∴由抛物线的对称性及单调性知:y1>y2,故④错误;
综上所述②③正确.
故答案为:②③.
点评 此题考查了二次函数的图象与系数的关系,抛物线的单调性、对称性及其应用问题;灵活运用有关知识来分析是解题关键.


科目:初中数学 来源: 题型:解答题
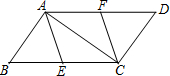 已知,如图,在?ABCD中,AC是对角线,AB=AC,点E、F分别是BC、AD的中点,连接AE,CF.
已知,如图,在?ABCD中,AC是对角线,AB=AC,点E、F分别是BC、AD的中点,连接AE,CF.查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 字母A | B. | 字母B | C. | 字母D | D. | 字母F |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 为缓解“停车难”的问题,某单位拟建造地下停车库,建筑设计师提供了该地下停车库的设计示意图,其中,AB⊥BD,∠BAD=18°,C在BD上,BC=0.5m.按规定,地下停车库坡道口上方要张贴限高标志,以便告知停车人车辆能否安全驶入,请你根据该图计算CD,CE的长,并标明限制高度.
为缓解“停车难”的问题,某单位拟建造地下停车库,建筑设计师提供了该地下停车库的设计示意图,其中,AB⊥BD,∠BAD=18°,C在BD上,BC=0.5m.按规定,地下停车库坡道口上方要张贴限高标志,以便告知停车人车辆能否安全驶入,请你根据该图计算CD,CE的长,并标明限制高度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在菱形ABCD中,对角线AC与BD相交于点O,MN过点O且与边AD、BC分别交于点M和点N.
如图,在菱形ABCD中,对角线AC与BD相交于点O,MN过点O且与边AD、BC分别交于点M和点N.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,树AB垂直于地面,为测树高,小明在C处,测得∠ACB=15°,他沿CB方向走了20米,到达D处,测得∠ADB=30°,你能帮助小明计算出树的高度吗?
如图,树AB垂直于地面,为测树高,小明在C处,测得∠ACB=15°,他沿CB方向走了20米,到达D处,测得∠ADB=30°,你能帮助小明计算出树的高度吗?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com