
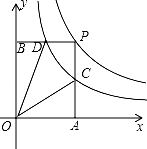
如图是函数y=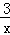 与函数y=
与函数y=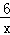 在第一象限内的图象,点P是y=
在第一象限内的图象,点P是y=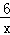 的图象上一动点,PA⊥x轴于点A,交y=
的图象上一动点,PA⊥x轴于点A,交y=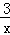 的图象于点C,PB⊥y轴于点B,交y=
的图象于点C,PB⊥y轴于点B,交y= 的图象于点D.
的图象于点D.
(1)求证:D是BP的中点;
(2)求四边形ODPC的面积.
【考点】反比例函数与一次函数的交点问题.
【分析】(1)根据函数图象上的点满足函数解析式,可得P、D点坐标,根据线段中点的定义,可得答案;
(2)根据图象割补法,可得面积的和差,可得答案.
【解答】(1)证明:∵点P在函数y=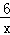 上,
上,
∴设P点坐标为( ,m).
,m).
∵点D在函数y=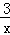 上,BP∥x轴,
上,BP∥x轴,
∴设点D坐标为( ,m),
,m),
由题意,得
BD= ,BP=
,BP= =2BD,
=2BD,
∴D是BP的中点.
(2)解:S四边形OAPB= •m=6,
•m=6,
设C点坐标为(x,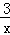 ),D点坐标为(
),D点坐标为( ,y),
,y),
S△OBD=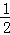 •y•
•y• =
=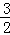 ,
,
S△OAC=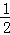 •x•
•x•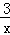 =
=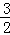 ,
,
S四边形OCPD=S四边形PBOA﹣S△OBD﹣S△OAC=6﹣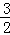 ﹣
﹣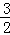 =3.
=3.
【点评】本题考查了反比例函数与一次函数的交点问题,利用了函数图象上的点满足函数解析式,线段中点的定义,图形割补法是求图形面积的重要方法.


科目:初中数学 来源: 题型:
已知二次函数y=ax2+bx+c的图象如图所示,有以下结论:①abc>0,②a﹣b+c<0,③2a=b,④4a+2b+c>0,⑤若点(﹣2,y1)和(﹣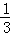 ,y2)在该图象上,则y1>y2.其中正确的结论是 (填入正确结论的序号).
,y2)在该图象上,则y1>y2.其中正确的结论是 (填入正确结论的序号).

查看答案和解析>>
科目:初中数学 来源: 题型:
已知两点M(3,2),N(-1, 3),点P是x轴上一动点,若使PM+PN最短,则点P的坐标应为
A. (0,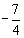 ) B. (
) B. (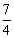 ,0) C. (
,0) C. (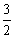 ,0) D. (
,0) D. (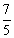 ,0)
,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
数学课上,同学们兴致勃勃地探讨着利用不同画图工具画角的平分线的方法.
小惠说:如图1,我用相同的两块含30° 角的直角三角板可以画角的平分线.画法如下:
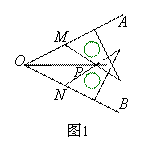 (1)在∠AOB 的两边上分别取点M,N,使OM=ON;
(1)在∠AOB 的两边上分别取点M,N,使OM=ON;
(2)把直角三角板按如图所示的位置放置,两斜边交于点P.
射线OP是∠AOB的平分线.
小旭说:我只用刻度尺就可以画角平分线.
请你也参与探讨,解决以下问题:
(1)小惠的做法正确吗?说明理由;
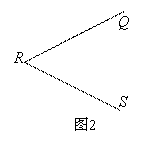
(2)请你和小旭一样,只用刻度尺画出图2中∠QRS的平分线,并简述画图的过程.
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
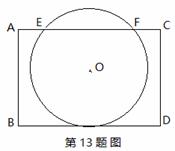
把球放在长方体纸盒内,球的一部分露出盒外,从正面看如图所示,⊙O与矩形ABCD的边BD,AC分别相切和相交(E,F是交点),已知EF=CD=8,则⊙O的半径为___________。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com