
已知二次函数y=ax2+bx+c的图象如图所示,有以下结论:①abc>0,②a﹣b+c<0,③2a=b,④4a+2b+c>0,⑤若点(﹣2,y1)和(﹣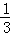 ,y2)在该图象上,则y1>y2.其中正确的结论是 (填入正确结论的序号).
,y2)在该图象上,则y1>y2.其中正确的结论是 (填入正确结论的序号).

②④
【考点】二次函数图象与系数的关系.
【分析】由图象可先判断a、b、c的符号,可判断①;由x=﹣1时函数的图象在x轴下方可判断②;由对称轴方程可判断③;由对称性可知当x=2时,函数值大于0,可判断④;结合二次函数的对称性可判断⑤;可得出答案.
【解答】解:
∵二次函数开口向下,且与y轴的交点在x轴上方,
∴a<0,c>0,
∵对称轴为x=1,
∴﹣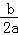 =1,
=1,
∴b=﹣2a>0,
∴abc<0,
故①、③都不正确;
∵当x=﹣1时,y<0,
∴a﹣b+c<0,
故②正确;
由抛物线的对称性可知抛物线与x轴的另一交点在2和3之间,
∴当x=2时,y>0,
∴4a+2b+c>0,
故④正确;
∵抛物线开口向下,对称轴为x=1,
∴当x<1时,y随x的增大而增大,
∵﹣2<﹣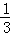 ,
,
∴y1<y2,
故⑤不正确;
综上可知正确的为②④,
故答案为:②④.
【点评】本题主要考查二次函数的性质,掌握二次函数的开口方向、对称轴、增减性是解题的关键,注意数形结合.


科目:初中数学 来源: 题型:
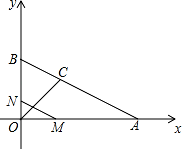
如图,已知点 A(4,0)、B(0,2),∠AOB 的平分线交 AB 于 C.动点 M 从 O 点出发,以每 秒 2 个单位长度的速度沿 x 轴向点 A 作匀速运动,同时动点 N 从 O 点出发,以每秒 1 个单位长度的 速度沿 y 轴向点 B 作匀速运动,点 P、Q 为点 M、N 关于直线 OC 的对称点,设 M 运动的时间为 t
(0<t<2)秒.
(1)求 C 点的坐标,并直接写出点 P、Q 的坐标(用含 t 的代数式表示); 运动过程中,
①是否存在某一时刻使得△CPQ 为等腰直角三角形?若存在,求出 t 的值;若不存在,请说明理由;
②设△CPQ 与△OAB 重叠部分的面积为 S,试求 S 关于 t 的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
某超市用3000元购进某种干果销售,由于销售状况良好,超市又调拨9000元资金购进该种干果,但这次的进价比第一次的进价提高了20%,购进干果数量是第一次的2倍还多300千克.如果超市按每千克9元的价格出售,当大部分干果售出后,余下的600千克按售价的8折售完.
(1)该种干果的第一次进价是每千克多少元?
(2)超市销售这种干果共盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,正比例函数y1=k1x的图象与反比例函数y2=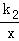 的图象相交于A,B两点,其中点A的横坐标为2,当y1>y2时,x的取值范围是( )
的图象相交于A,B两点,其中点A的横坐标为2,当y1>y2时,x的取值范围是( )
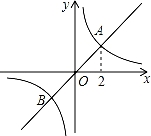
A.x<﹣2或x>2 B.x<﹣2或0<x<2
C.﹣2<x<0或0<x<﹣2 D.﹣2<x<0或x>2
查看答案和解析>>
科目:初中数学 来源: 题型:
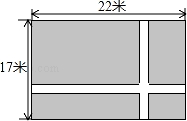
如图,在一块长为22米、宽为17米的矩形地面上,要修建同样宽的两条互相垂直的道路(两条道路各与矩形的一条边平行),剩余部分种上草坪,使草坪面积为300平方米.若设道路宽为x米,则根据题意可列出方程为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
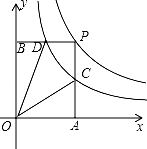
如图是函数y=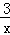 与函数y=
与函数y=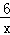 在第一象限内的图象,点P是y=
在第一象限内的图象,点P是y=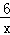 的图象上一动点,PA⊥x轴于点A,交y=
的图象上一动点,PA⊥x轴于点A,交y=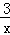 的图象于点C,PB⊥y轴于点B,交y=
的图象于点C,PB⊥y轴于点B,交y=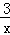 的图象于点D.
的图象于点D.
(1)求证:D是BP的中点;
(2)求四边形ODPC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com