
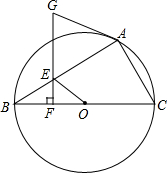
 如图,已知,⊙O为△ABC的外接圆,BC为直径,点E在AB边上,过点E作EF⊥BC,延长FE交⊙O的切线AG于点G.
如图,已知,⊙O为△ABC的外接圆,BC为直径,点E在AB边上,过点E作EF⊥BC,延长FE交⊙O的切线AG于点G.分析 (1)根据切线的性质和等腰三角形的性质即可得到结论;
(2)根据勾股定理求得BC=10,然后根据△BEF∽△BCA.对应边成比例求得EF=1.8,BF=2.4,进而求得OF=2.6,应用勾股定理求得即可.
解答 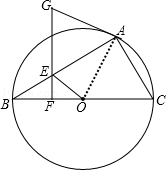 (1)证明:连接OA,
(1)证明:连接OA,
∵AG切⊙O点A,
∴∠GAO=90°,
∴∠BAO+∠GAE=90°,
∵EF⊥BC,
∴∠ABO+∠BEF=90°,
∵OA=OB,
∴∠ABO=∠BAO,
∴∠GAE=∠BEF,
∵∠BEF=∠GEA,
∴∠GEA=∠GAE,
∴GA=GE;
(2)解:∵BC为直径,
∴∠BAC=90°,AC=6,AB=8,
∴BC=10,
∵∠EBF=∠CBA,∠BFE=∠BAC,
∴△BEF∽△BCA,
∴$\frac{BF}{BA}=\frac{BE}{BC}=\frac{EF}{AC}$,
∴EF=$\frac{9}{5}$,BF=$\frac{12}{5}$,
∴OF=OB-BF=5-$\frac{12}{5}$=$\frac{13}{5}$,
∴OE=$\sqrt{{EF}^{2}{+OF}^{2}}$=$\sqrt{10}$.
点评 本题考查了等腰三角形的性质,切线的判定,勾股定理的应用,三角形相似的判定和性质等,熟练掌握性质定理是解题的关键.


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:初中数学 来源: 题型:填空题
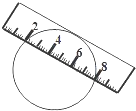 如图,一宽为2cm的刻度尺在圆上移动,当刻度尺的一边与圆相切时,另一边与圆两个交点处的读数恰好为“2”和“8”(单位:cm),则该圆的半径为$\frac{13}{4}$cm.
如图,一宽为2cm的刻度尺在圆上移动,当刻度尺的一边与圆相切时,另一边与圆两个交点处的读数恰好为“2”和“8”(单位:cm),则该圆的半径为$\frac{13}{4}$cm.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=3x2+12x+15 | B. | y=3x2-12x+15 | C. | y=3x2+12x+9 | D. | y=3x2-12x+9 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 射线(不含端点) | B. | 线段(不含端点) | C. | 直线 | D. | 抛物线的一部分 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a=2012 | B. | a<2012 | C. | a>2012 | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
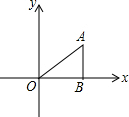 如图,在△ABO中,AB⊥OB,OB=$\sqrt{3}$,AB=1.将△ABO绕O点旋转90°后得到△A1B1O,则点A1的坐标为( )
如图,在△ABO中,AB⊥OB,OB=$\sqrt{3}$,AB=1.将△ABO绕O点旋转90°后得到△A1B1O,则点A1的坐标为( )| A. | (-1,$\sqrt{3}$) | B. | (-1,$\sqrt{3}$)或(1,-$\sqrt{3}$) | C. | (-1,-$\sqrt{3}$) | D. | (-1,-$\sqrt{3}$)或(-$\sqrt{3}$,-1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com