Question

【题目】如图，在正方形ABCD内有一折线段，其中AE⊥EF，EF⊥FC，并且AE=4，EF=8，FC=12，则正方形与其外接圆形成的阴影部分的面积为 ．

Answer 1

【答案】80π﹣160
【解析】解：连接AC，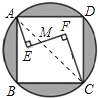

∵AE丄EF，EF丄FC，
∴∠E=∠F=90°，
∵∠AME=∠CMF（对顶角相等），
∴△AEM∽△CFM，
∴ ，
∵AE=4，FC=12，
∴ ，
∴EM=2，FM=6，
在Rt△AEM中，AM= =2 ，在Rt△FCM中，CM= =6 ，∴AC=8 ，在Rt△ABC中，AB=ACsin45°=8 × =4 ，
∴S正方形ABCD=AB2=160，
圆的面积为：π（ ）2=80π，
∴正方形与其外接圆之间形成的阴影部分的面积为80π﹣160．
所以答案是：80π﹣160．
【考点精析】认真审题，首先需要了解勾股定理的概念(直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2)，还要掌握正方形的性质(正方形四个角都是直角，四条边都相等；正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角；正方形的一条对角线把正方形分成两个全等的等腰直角三角形；正方形的对角线与边的夹角是45o；正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形)的相关知识才是答题的关键．