
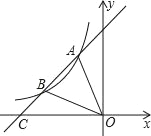
【题目】如图,一次函数y=kx+b与反比例函数y=![]() (x<0)的图象相交于点A、点B,与X轴交于点C,其中点A(﹣1,3)和点B(﹣3,n).
(x<0)的图象相交于点A、点B,与X轴交于点C,其中点A(﹣1,3)和点B(﹣3,n).
(1)填空:m= ,n= .
(2)求一次函数的解析式和△AOB的面积.
(3)根据图象回答:当x为何值时,kx+b≥![]() (请直接写出答案) .
(请直接写出答案) .
【答案】(1) ﹣3,1;(2) y=x+4,4;(3)﹣3≤x≤﹣1.
【解析】
(1)已知反比例函数y=![]() 过点A(﹣1,3),B(﹣3,n)分别代入求得m、n的值即可;(2)用待定系数法求出一次函数的解析式,再求得一次函数与x轴的交点坐标,根据S△AOB=S△AOC﹣S△BOC即可求得△AOB的面积;(3)观察图象,确定一次函数图象在反比例函数图象上方时对应的x的取值范围即可.
过点A(﹣1,3),B(﹣3,n)分别代入求得m、n的值即可;(2)用待定系数法求出一次函数的解析式,再求得一次函数与x轴的交点坐标,根据S△AOB=S△AOC﹣S△BOC即可求得△AOB的面积;(3)观察图象,确定一次函数图象在反比例函数图象上方时对应的x的取值范围即可.
(1)∵反比例函数y=![]() 过点A(﹣1,3),B(﹣3,n)
过点A(﹣1,3),B(﹣3,n)
∴m=3×(﹣1)=﹣3,m=﹣3n
∴n=1
故答案为﹣3,1
(2)设一次函数解析式y=kx+b,且过(﹣1,3),B(﹣3,1)
∴![]()
解得:![]()
∴解析式y=x+4
∵一次函数图象与x轴交点为C
∴0=x+4
∴x=﹣4
∴C(﹣4,0)
∵S△AOB=S△AOC﹣S△BOC
∴S△AOB=![]() ×4×3﹣
×4×3﹣![]() ×4×1=4
×4×1=4
(3)∵kx+b≥![]()
∴一次函数图象在反比例函数图象上方
∴﹣3≤x≤﹣1
故答案为﹣3≤x≤﹣1


科目:初中数学 来源: 题型:
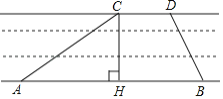
【题目】京杭大运河是世界文化遗产.综合实践活动小组为了测出某段运河的河宽(岸沿是平行的),如图,在岸边分别选定了点A、B和点C、D,先用卷尺量得AB=160m,CD=40m,再用测角仪测得∠CAB=30°,∠DBA=60°,求该段运河的河宽(即CH的长).
查看答案和解析>>
科目:初中数学 来源: 题型:
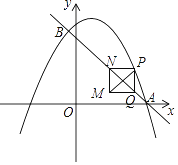
【题目】如图,在平面直角坐标系中,直线y=﹣x+3与抛物线![]() 交于A、B两点,点A在x轴上,点B的横坐标为
交于A、B两点,点A在x轴上,点B的横坐标为![]() .动点P在抛物线上运动(不与点A、B重合),过点P作y轴的平行线,交直线AB于点Q.当PQ不与y轴重合时,以PQ为边作正方形PQMN,使MN与y轴在PQ的同侧,连结PM.设点P的横坐标为m.
.动点P在抛物线上运动(不与点A、B重合),过点P作y轴的平行线,交直线AB于点Q.当PQ不与y轴重合时,以PQ为边作正方形PQMN,使MN与y轴在PQ的同侧,连结PM.设点P的横坐标为m.
(1)求b、c的值.
(2)当点N落在直线AB上时,直接写出m的取值范围.
(3)当点P在A、B两点之间的抛物线上运动时,设正方形PQMN的周长为C,求C与m之间的函数关系式,并写出C随m增大而增大时m的取值范围.
(4)当△PQM与坐标轴有2个公共点时,直接写出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
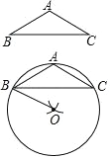
【题目】下面是“作顶角为 120°的等腰三角形的外接圆”的尺规作图过程.已知:△ABC,AB=AC,∠A=120°.求作:△ABC 的外接圆.作法:(1)分别以点 B 和点 C 为圆心,AB 的长为半径作弧,两弧的一个交点为 O;(2)连接 BO;(3)以 O 为圆心,BO 为半径作⊙O.⊙O 即为所求作的圆.请回答:该尺规作图的依据是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】假设北碚万达广场地下停车场有5个出入口,每天早晨6点开始对外停车且此时车位空置率为75%,在每个出入口的车辆数均是匀速出入的情况下,如果开放2个进口和3个出口,8小时车库恰好停满;如果开放3个进口和2个出口,2小时车库恰好停满.2019年元旦节期间,由于商场人数增多,早晨6点时的车位空置率变为60%,又因为车库改造,只能开放2个进口和1个出口,则从早晨6点开始经过________小时车库恰好停满.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读对话,解答问题:

(1)分别用a、b表示小冬从小丽、小兵袋子中抽出的卡片上标有的数字,请用树状图法或列表法写出(a,b)的所有取值;
(2)求在(a,b)中使关于x的一元二次方程x2﹣ax+2b=0有实数根的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“每天锻炼一小时,健康生活一辈子”.为了选拔“阳光大课间”领操员,学校组织初中三个年级推选出来的15名领操员进行比赛,成绩如下表:
成绩/分 | 7 | 8 | 9 | 10 |
人数/人 | 2 | 5 | 4 | 4 |
(1)这组数据的众数是多少,中位数是多少.
(2)已知获得2018年四川省南充市的选手中,七、八、九年级分别有1人、2人、1人,学校准备从中随机抽取两人领操,求恰好抽到八年级两名领操员的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系内,以原点O为圆心,1为半径作圆,点P在直线![]() 上运动,过点P作该圆的一条切线,切点为A,则PA的最小值为
上运动,过点P作该圆的一条切线,切点为A,则PA的最小值为![]()
![]()
A. 3 B. 2 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小西“过直线外一点作这条直线的垂线”的尺规作图过程.
已知:直线l及直线l外一点P.
求作:直线PQ,使得PQ⊥l.
做法:如图,
①在直线l的异侧取一点K,以点P为圆心,PK长为半径画弧,交直线l于点A,B;
②分别以点A,B为圆心,大于![]() AB的同样长为半径画弧,两弧交于点Q(与P点不重合);
AB的同样长为半径画弧,两弧交于点Q(与P点不重合);
③作直线PQ,则直线PQ就是所求作的直线.
根据小西设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:∵PA= ,QA= ,
∴PQ⊥l( )(填推理的依据).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com