Question

11．如图，在扇形OAB中，∠AOB=105°，半径OA=18，将扇形OAB沿过点B的直线折叠，点O恰好落在$\widehat{AB}$上的点D处，折痕交OA于点C，则折痕BC的长为9+9$\sqrt{3}$．

Answer 1

分析 连接OD，首先证明△OBD是等边三角形，分别在Rt△EOB，Rt△EOC中，求出CE、EB即可解决问题．

解答 解：连接OD，
由题意得，OB=BD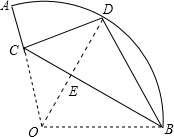，OD⊥BC，
∵OD=OB=BD，
∴三角形OBD为等边三角形，
∴∠DOB=60°，
∵∠AOB=105°，
∴∠COE=45°，
在Rt△OBE中，∵∠OEB=90°，OB=OA=18，∠EOB=60°，
∴∠EBO=30°，
∴OE=$\frac{1}{2}$OB=9，EB=$\sqrt{O{B}^{2}-O{E}^{2}}$=9$\sqrt{3}$，
在Rt△CEO中，∵∠CEO=90°，∠COE=45°，
∴∠OCE=∠EOC=45°，
∴CE=OE=9，
∴BC=EC+EB=9+9$\sqrt{3}$．
故答案为9+9$\sqrt{3}$．

点评 本题考查翻折变换、等边三角形的性质、直角三角形的性质，勾股定理等知识，解题的关键是灵活运用这些知识解决问题，属于中考常考题型．