
在□ABCD中,AE、BF分别平分∠DAB和∠ABC,交CD于点E、F,AE、BF相交于点M.
(1)试说明:AE⊥BF;
(2)判断线段DF与CE的大小关系,并说明理由.

(1)证明见解析;(2)DF=CE.理由见解析.
【解析】
试题分析:(1)因为AE,BF分别是∠DAB,∠ABC的角平分线,那么就有∠MAB=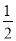 ∠DAB,∠MBA=
∠DAB,∠MBA=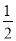 ∠ABC,而∠DAB与∠ABC是同旁内角互补,所以,能得到∠MAB+∠MBA=90°,即得证.
∠ABC,而∠DAB与∠ABC是同旁内角互补,所以,能得到∠MAB+∠MBA=90°,即得证.
(2)两条线段相等.利用平行四边形的对边平行,以及角平分线的性质,可以得到△ADE和△BCF都是等腰三角形,那么就有CF=BC=AD=DE,再利用等量减等量差相等,可证.
(1)∵在?ABCD中,AD∥BC,
∴∠DAB+∠ABC=180°.(1分)
∵AE、BF分别平分∠DAB和∠ABC,
∴∠DAB=2∠BAE,∠ABC=2∠ABF.
∴2∠BAE+2∠ABF=180°.
即∠BAE+∠ABF=90°.
∴∠AMB=90°.
∴AE⊥BF.
(2)线段DF与CE是相等关系,即DF=CE,
∵在?ABCD中,CD∥AB,
∴∠DEA=∠EAB.
又∵AE平分∠DAB,
∴∠DAE=∠EAB.
∴∠DEA=∠DAE.
∴DE=AD.(6分)
同理可得,CF=BC.
又∵在?ABCD中,AD=BC,
∴DE=CF.
∴DE-EF=CF-EF.
即DF=CE.
考点:1.相似三角形的判定与性质;2.角平分线的性质;3.平行四边形的性质.


科目:初中数学 来源:2013-2014学年江苏省盐城市亭湖区中考一模数学试卷(解析版) 题型:选择题
如图,点A的坐标为(6,0),点B为y轴的负半轴上的一个动点,分别以OB,AB为直角边在第三、第四象限作等腰Rt△OBF,等腰Rt△ABE,连接EF交y轴于P点,当点B在y轴上移动时,PB的长度为( )

A、2 B、3
C、4 D、PB的长度随点B的运动而变化
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省泰州市姜堰区中考适应性考试数学试卷(解析版) 题型:解答题
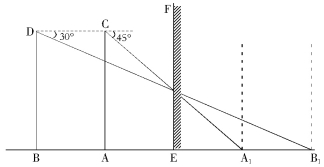
如图,当小华站立在镜子EF前A处时(镜子直立在地面上),他看自己的脚在镜中的像A1时的俯角为45°.若小华向后退0.5m到B处,这时他看自己的脚在镜中的像B1的俯角为30°.求小华的眼睛到地面的距离(结果精确到0.1m,参考数据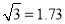 );
);
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省江阴市要塞片九年级下学期期中考试数学试卷(解析版) 题型:解答题
对正方形ABCD分划如图①,其中E、F分别是BC、CD的中点,M、N、G分别是OB、OD、EF的中点,沿分划线可以剪出一副由七块部件组成的“七巧板”.
(1)如果设正方形OGFN的边长为l,这七块部件的各边长中,从小到大的四个不同值分别为l、x1、x2、x3,那么x1= ;各内角中最小内角是 度,最大内角是 度;用它们拼成的一个五边形如图②,其面积是 ,
(2)请用这副七巧板,既不留下一丝空白,又不相互重叠,拼出2种边数不同的凸多边形,画在下面格点图中,并使凸多边形的顶点落在格点图的小黑点上(格点图中,上下、左右相邻两点距离都为1).
注:不能拼成与图①或②全等的多边形!



查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省江阴市要塞片九年级下学期期中考试数学试卷(解析版) 题型:选择题
如图,为估计池塘岸边A、B两点的距离,小方在池塘的一侧选取一点O,测得OA=8米,OB=6米,A、B间的距离不可能是( )
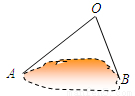
A.12米 B.10米 C. 15米 D.8米
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省江阴市九年级下学期期中考试数学试卷(解析版) 题型:选择题
平面直角坐标系中,四边形ABCD的顶点坐标分别是A(-3,0)、B(0,2)、C(3,0)、D(0,-2),则四边形ABCD是 ( )
A.矩形 B.菱形 C.正方形 D.梯形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com