
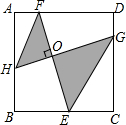
 如图,在正方形ABCD中,点H,E,G,F分别在AB,BC,CD,DA上.若EF⊥HG于点O,HF∥GE,BE=EC=4,EO=2FO,图中阴影部分的面积$\frac{170}{9}$.
如图,在正方形ABCD中,点H,E,G,F分别在AB,BC,CD,DA上.若EF⊥HG于点O,HF∥GE,BE=EC=4,EO=2FO,图中阴影部分的面积$\frac{170}{9}$. 分析 易得△AHF∽△CGE,所以$\frac{AF}{CE}$=$\frac{FH}{EG}$=$\frac{FO}{OE}$,由EC=2得AF=1,过F作FP⊥BC于P,根据勾股定理得EF=2$\sqrt{17}$,因为FH∥EG,所以$\frac{FO}{OE}$=$\frac{HO}{HG}$,知EF=GH,所以FO=HO,再求得△FOH与三角形△的面积相加即可.
解答 解:将FE平移到AM处,则AM∥EF,AM=EF.
将GH平移到DN处,则DN∥GH,DN=GH.
∵EF⊥GH,
∴AM⊥DN,
在△ABM与△DAN中,
$\left\{\begin{array}{l}{BAM=∠ADN}\\{AB=DA}\\{∠ABM=∠DAN}\end{array}\right.$,
∴△ABM≌△DAN(ASA),
则AM=DN,
∴EF=GH;
∵四边形ABCD是正方形,
∴AB∥CD
∴∠AHO=∠CGO
∵FH∥EG
∴∠FHO=∠EGO
∴∠AHF=∠CGE
∴△AHF∽△CGE
∴$\frac{AF}{CE}$=$\frac{FH}{EG}$=$\frac{FO}{OE}$,
∵EC=4
∴AF=2
过F作FP⊥BC于P,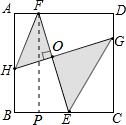
根据勾股定理得EF=2$\sqrt{17}$,
∵FH∥EG,
∴$\frac{FO}{OE}$=$\frac{HO}{HG}$,
∵EF=GH,
∴FO=HO.
∴S△FOH=$\frac{1}{2}$FO2=$\frac{1}{2}$×($\frac{1}{3}$EF)2,S△EOG=$\frac{1}{2}$×($\frac{2}{3}$EF)2,
∴阴影部分面积为$\frac{170}{9}$.
故答案是:$\frac{170}{9}$.
点评 本题考查了三角形的综合知识.用到全等三角形的判定与性质、相似三角形的判定与性质、勾股定理等综合性较强,难度较大.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com