
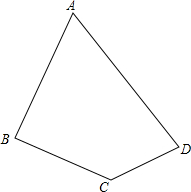
 如图,已知∠A+∠C=180°,∠B+∠D=180°,求证:点A,B,C,D四点共圆.
如图,已知∠A+∠C=180°,∠B+∠D=180°,求证:点A,B,C,D四点共圆. 分析 过A,B,D作圆O,假设C不在圆O上,则C在圆外或圆内,分点C在圆外和点C在圆内两种情况利用反证法证得A,B,C,D四点共圆即可.
解答 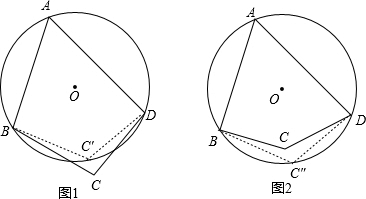 证明:过A,B,D作圆O,假设C不在圆O上,则C在圆外或圆内,
证明:过A,B,D作圆O,假设C不在圆O上,则C在圆外或圆内,
若C在圆外,如图1,设BC交圆O于C′,
根据圆内接四边形的性质得∠A+∠DC′B=180°,
∵∠A+∠C=180°,
∴∠DC′B=∠C,
这与三角形外角定理矛盾,故C不可能在圆外;
类似地(如图2)点C不可能在圆内;
∴C在圆O上,也即A,B,C,D四点共圆.
点评 本题考查了四点共圆的知识及反证法的知识,用反证法证明结论时,首先否定结论,然后从假设出发得到矛盾,从而肯定结论,难度中等.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在平面直角坐标系中,四边形ABCD的顶点均在网格点上,将四边形ABCD先向左平移3个单位,再向上平移2个单位,那么点A的对应点A′的坐标是( )
如图,在平面直角坐标系中,四边形ABCD的顶点均在网格点上,将四边形ABCD先向左平移3个单位,再向上平移2个单位,那么点A的对应点A′的坐标是( )| A. | (6,1) | B. | (0,1) | C. | (0,-3) | D. | (6,-3) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
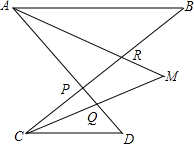 如图,∠B=36°,∠D=50°,AM,CM分别平分∠BAD和∠BCD,AM交BC于点R,CM交AD于点Q,BC与AD交于点P,求∠M的度数.
如图,∠B=36°,∠D=50°,AM,CM分别平分∠BAD和∠BCD,AM交BC于点R,CM交AD于点Q,BC与AD交于点P,求∠M的度数.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  | B. | 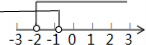 | ||
| C. | 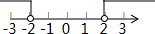 | D. | 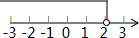 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
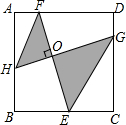 如图,在正方形ABCD中,点H,E,G,F分别在AB,BC,CD,DA上.若EF⊥HG于点O,HF∥GE,BE=EC=4,EO=2FO,图中阴影部分的面积$\frac{170}{9}$.
如图,在正方形ABCD中,点H,E,G,F分别在AB,BC,CD,DA上.若EF⊥HG于点O,HF∥GE,BE=EC=4,EO=2FO,图中阴影部分的面积$\frac{170}{9}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
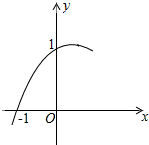 如图是二次函数y=ax2+bx+c是图象的一部分,记M=a+b,则M的取值范围是( )
如图是二次函数y=ax2+bx+c是图象的一部分,记M=a+b,则M的取值范围是( )| A. | -1<M<0 | B. | -1<M<1 | C. | 0<M<1 | D. | 不能确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com