
分析 (1)首先解每个不等式,两个不等式的解集的公共部分就是不等式组的解集;
(2)首先化成不等式组的形式,解每个不等式,两个不等式的解集的公共部分就是不等式组的解集.
解答 解:(1)$\left\{\begin{array}{l}{\frac{1-x}{2}>\frac{x-6}{3}…①}\\{3x-2<4x+1…②}\end{array}\right.$,
解①得:x<3,
解②得:x>-3,
则不等式组的解集是:-3<x<3;
(2)原式即$\left\{\begin{array}{l}{\frac{1-2x}{5}≥-1…①}\\{\frac{1-2x}{5}<2…②}\end{array}\right.$,
解①得:x≤3,
解②得:x>-$\frac{9}{2}$.
则x的范围是:-$\frac{9}{2}$<x≤3.
点评 本题考查的是一元一次不等式组的解,解此类题目常常要结合数轴来判断.还可以观察不等式的解,若x>较小的数、<较大的数,那么解集为x介于两数之间.


科目:初中数学 来源: 题型:解答题
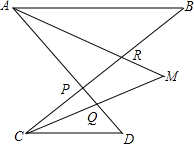 如图,∠B=36°,∠D=50°,AM,CM分别平分∠BAD和∠BCD,AM交BC于点R,CM交AD于点Q,BC与AD交于点P,求∠M的度数.
如图,∠B=36°,∠D=50°,AM,CM分别平分∠BAD和∠BCD,AM交BC于点R,CM交AD于点Q,BC与AD交于点P,求∠M的度数.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  | B. | 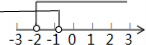 | ||
| C. | 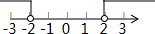 | D. | 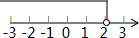 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
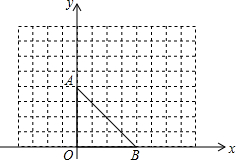 如图,点A的坐标是(0,4),点B的坐标是(4,0).
如图,点A的坐标是(0,4),点B的坐标是(4,0).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
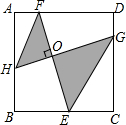 如图,在正方形ABCD中,点H,E,G,F分别在AB,BC,CD,DA上.若EF⊥HG于点O,HF∥GE,BE=EC=4,EO=2FO,图中阴影部分的面积$\frac{170}{9}$.
如图,在正方形ABCD中,点H,E,G,F分别在AB,BC,CD,DA上.若EF⊥HG于点O,HF∥GE,BE=EC=4,EO=2FO,图中阴影部分的面积$\frac{170}{9}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
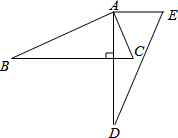 如图,将△ABC绕点A逆时针旋转一定角度,得到△ADE,且AD⊥BC.若∠CAE=65°,∠E=60°,则∠BAC的大小为( )
如图,将△ABC绕点A逆时针旋转一定角度,得到△ADE,且AD⊥BC.若∠CAE=65°,∠E=60°,则∠BAC的大小为( )| A. | 60° | B. | 75° | C. | 85° | D. | 95° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com