
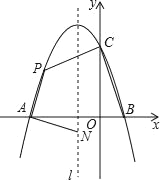
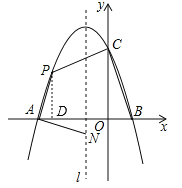
【题目】如图,抛物线y=ax2+bx+c与x轴交于点A和点B(1,0),与y轴交于点C(0,3),其对称轴l为x=﹣1.
(1)求抛物线的解析式并写出其顶点坐标;
(2)若动点P在第二象限内的抛物线上,动点N在对称轴l上.
①当PA⊥NA,且PA=NA时,求此时点P的坐标;
②当四边形PABC的面积最大时,求四边形PABC面积的最大值及此时点P的坐标.
【答案】(1)y=﹣(x+1)2+4,顶点坐标为(﹣1,4);(2)①点P(﹣![]() ﹣1,2);②P(﹣
﹣1,2);②P(﹣![]() ,
, ![]() )
)
【解析】试题分析:(1)将B、C的坐标代入已知的抛物线的解析式,由对称轴为![]() 即可得到抛物线的解析式;
即可得到抛物线的解析式;
(2)①首先求得抛物线与x轴的交点坐标,然后根据已知条件得到PD=OA,从而得到方程求得x的值即可求得点P的坐标;
②![]() ,表示出来得到二次函数,求得最值即可.
,表示出来得到二次函数,求得最值即可.
试题解析:(1)∵抛物线![]() 与x轴交于点A和点B(1,0),与y轴交于点C(0,3),其对称轴l为
与x轴交于点A和点B(1,0),与y轴交于点C(0,3),其对称轴l为![]() ,∴
,∴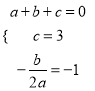 ,解得:
,解得: 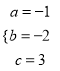 ,∴二次函数的解析式为
,∴二次函数的解析式为![]() =
=![]() ,∴顶点坐标为(﹣1,4);
,∴顶点坐标为(﹣1,4);
(2)令![]() ,解得
,解得![]() 或
或![]() ,∴点A(﹣3,0),B(1,0),作PD⊥x轴于点D,∵点P在
,∴点A(﹣3,0),B(1,0),作PD⊥x轴于点D,∵点P在![]() 上,∴设点P(x,
上,∴设点P(x, ![]() ),
),
①∵PA⊥NA,且PA=NA,∴△PAD≌△AND,∴OA=PD,即![]() ,解得x=
,解得x=![]() (舍去)或x=
(舍去)或x=![]() ,∴点P(
,∴点P(![]() ,2);
,2);
②设P(x,y),则![]() ,∵
,∵![]()
=![]() OBOC+
OBOC+![]() ADPD+
ADPD+![]() (PD+OC)OD=
(PD+OC)OD=![]() =
= ![]()
=![]() =
=![]() =
=![]() ,
,
∴当x=![]() 时,
时, ![]() =
=![]() ,当x=
,当x=![]() 时,
时, ![]() =
=![]() ,此时P(
,此时P(![]() ,
, ![]() ).
).


科目:初中数学 来源: 题型:
【题目】甲、乙两车先后从“深圳书城”出发,沿相同的路线到距书城240km的某市.因路况原因,甲车行驶的路程y (km)与甲车行驶的时间x (h)的函数关系图象为折线 O-A-B, 乙车行驶的路程y (km)与甲车行驶的时间x(h)的函数关系图象为线段CD.
(1)求线段AB所在直线的函数表达式;
(2)①乙车比甲车晚出发 小时;
②乙车出发多少小时后追上甲车?
(3)乙车出发多少小时后甲、乙两车相距10千米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是自动喷灌设备的水管,点
是自动喷灌设备的水管,点![]() 在地面,点
在地面,点![]() 高出地面
高出地面![]() 米.在
米.在![]() 处有一自动旋转的喷水头,在每一瞬间,喷出的水流呈抛物线状,喷头
处有一自动旋转的喷水头,在每一瞬间,喷出的水流呈抛物线状,喷头![]() 与水流最高点
与水流最高点![]() 的连线与水平线成
的连线与水平线成![]() 角,水流的最高点
角,水流的最高点![]() 与喷头
与喷头![]() 高出
高出![]() 米,在如图的坐标系中,水流的落地点
米,在如图的坐标系中,水流的落地点![]() 到点
到点![]() 的距离是________米.
的距离是________米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两种机器人都被用来搬运化工原料,A型机器人比B型机器人每小时多搬运30kg,A型机器人搬运900kg与B型机器人搬运600kg所用时间相等,两种机器人每小时分别搬运多少化工原料?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小麦改良品种后平均每公顷增加产量a吨,原来产m吨小麦的一块土地,现在小麦的总产量增加了20吨.
(1)当a=0.8,m=100时,原来和现在小麦的平均每公顷产量各是多少?
(2)请直接接写出原来小麦的平均每公顷产量是 吨,现在小麦的平均每公顷产量是 吨;(用含a、m的式于表示)
(3)在这块土地上,小麦的改良品种成熟后,甲组收割完需n小时,乙组比甲组少用0.5小时就能收割完,求两组一起收割完这块麦田需要多少小时?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com