
【题目】如图,![]() 是自动喷灌设备的水管,点
是自动喷灌设备的水管,点![]() 在地面,点
在地面,点![]() 高出地面
高出地面![]() 米.在
米.在![]() 处有一自动旋转的喷水头,在每一瞬间,喷出的水流呈抛物线状,喷头
处有一自动旋转的喷水头,在每一瞬间,喷出的水流呈抛物线状,喷头![]() 与水流最高点
与水流最高点![]() 的连线与水平线成
的连线与水平线成![]() 角,水流的最高点
角,水流的最高点![]() 与喷头
与喷头![]() 高出
高出![]() 米,在如图的坐标系中,水流的落地点
米,在如图的坐标系中,水流的落地点![]() 到点
到点![]() 的距离是________米.
的距离是________米.

【答案】![]()
【解析】
根据所建坐标系,易知B点坐标和顶点C的坐标,设抛物线解析式为顶点式,可求表达式,求AD长就是求y=0是x的值.
如图,建立直角坐标系,过C点作CE⊥y轴于E,过C点作CF⊥x轴于F,
∴B(0,1.5),
∴∠CBE=45°,
∴EC=EB=2米,
∵CF=AB+BE=2+1.5=3.5,
∴C(2,3.5)
设抛物线解析式为:y=a(x-2)2+3.5,
又∵抛物线过点B,
∴1.5=a(0-2)2+3.5
∴a=-![]() ,
,
∴y=-![]() (x-2)2+3.5=-
(x-2)2+3.5=-![]() x2+2x+
x2+2x+![]() ,
,
∴所求抛物线解析式为:y=-![]() x2+2x+
x2+2x+![]() ,
,
∵抛物线与x轴相交时,y=0,
∴![]() ,
,
∴x1=![]() ,x2=
,x2=![]() (舍去)
(舍去)
∴D(![]() ,0)
,0)
∴水流落点D到A点的距离为:![]() 米.
米.

故答案为:![]()


科目:初中数学 来源: 题型:
【题目】如图,已知:在![]() 中,
中,![]() ,
,![]() .
.

(1)作![]() 的平分线BD,交AC于点D,作AB的中点E(要求:尺规作图,保留作图痕迹,不必写作法和证明);
的平分线BD,交AC于点D,作AB的中点E(要求:尺规作图,保留作图痕迹,不必写作法和证明);
(2)连接DE,判定直线AB与DE的位置关系,并对结论给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是两个可以自由转动的由红、蓝两色构成的转盘,其中转盘![]() 的蓝色部分占整个转盘的
的蓝色部分占整个转盘的![]() ,转盘
,转盘![]() 中的蓝色占整个转盘的
中的蓝色占整个转盘的![]() .转动转盘,转盘停止后指针所指颜色就是转出的颜色,现在甲、乙两个人做游戏.
.转动转盘,转盘停止后指针所指颜色就是转出的颜色,现在甲、乙两个人做游戏.
![]() 甲转动转盘
甲转动转盘![]() ,乙转动转盘
,乙转动转盘![]() ,每人转动十次,谁转出的红色次数多谁获胜.你认为这个游戏公平吗?如果不公平,谁容易获胜,请说明理由;
,每人转动十次,谁转出的红色次数多谁获胜.你认为这个游戏公平吗?如果不公平,谁容易获胜,请说明理由;
![]() 小明提出下面的改进方案:由第三个人来转动上面的两个转盘,如果两个转盘都转出了红色,则甲赢,否则乙赢,请你帮小明设计一种替代试验的方法,并写出试验的步骤.
小明提出下面的改进方案:由第三个人来转动上面的两个转盘,如果两个转盘都转出了红色,则甲赢,否则乙赢,请你帮小明设计一种替代试验的方法,并写出试验的步骤.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知矩形![]() 的边
的边![]() ,
,![]() ,现将矩形
,现将矩形![]() 如图放在直线
如图放在直线![]() 上,且沿着
上,且沿着![]() 向右作无滑动地翻滚,当它翻滚到位置
向右作无滑动地翻滚,当它翻滚到位置![]() 时,计算:
时,计算:
![]()
![]() 顶点
顶点![]() 所经过的路线长为________;
所经过的路线长为________;
![]() 点
点![]() 经过的路线与直线
经过的路线与直线![]() 所围成的面积为________.
所围成的面积为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,BD=CE,将线段AE沿AC翻折,得到线段AM,连结EM交AC于点N,连结DM、CM以下说法:①AD=AM,②∠MCA=60°,③CM=2CN,④MA=DM中,正确的有( )

A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
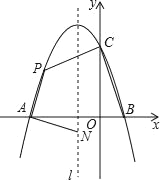
【题目】如图,抛物线y=ax2+bx+c与x轴交于点A和点B(1,0),与y轴交于点C(0,3),其对称轴l为x=﹣1.
(1)求抛物线的解析式并写出其顶点坐标;
(2)若动点P在第二象限内的抛物线上,动点N在对称轴l上.
①当PA⊥NA,且PA=NA时,求此时点P的坐标;
②当四边形PABC的面积最大时,求四边形PABC面积的最大值及此时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂准备用图甲所示的A型正方形板材和B型长方形板材,制作成图乙所示的竖式和横式两种无盖箱子.
(1)若该工厂准备用不超过10000元的资金去购买A,B两种型号板材,并全部制作竖式箱子,已知A型板材每张30元,B型板材每张90元,求最多可以制作竖式箱子多少只?
(2)若该工厂仓库里现有A型板材65张、B型板材110张,用这批板材制作两种类型的箱子,问制作竖式和横式两种箱子各多少只,恰好将库存的板材用完?
(3)若该工厂新购得65张规格为3×3m的C型正方形板材,将其全部切割成A型或B型板材(不计损耗),用切割成的板材制作两种类型的箱子,要求竖式箱子不少于20只,且材料恰好用完,则能制作两种箱子共 只.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=x2﹣2x﹣3与交y轴负半轴于C点,直线y=kx+2交抛物线于E、F两点(E点在F点左边).使△CEF被y轴分成的两部分面积差为5,则k的值为_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com