
【题目】如图,AE∥BF,AC平分∠BAE,且交BF于点C,BD平分∠ABF,且交AE于点D,连接CD. 
(1)求证:四边形ABCD是菱形;
(2)若∠ADB=30°,BD=6,求AD的长.
【答案】
(1)证明:∵AE∥BF,
∴∠ADB=∠CBD,
又∵BD平分∠ABF,
∴∠ABD=∠CBD,
∴∠ABD=∠ADB,
∴AB=AD,
同理:AB=BC,
∴AD=BC,
∴四边形ABCD是平行四边形,
又∵AB=AD,
∴四边形ABCD是菱形;
(2)解:∵四边形ABCD是菱形,BD=6,
∴AC⊥BD,OD=OB= ![]() BD=3,
BD=3,
∵∠ADB=30°,
∴cos∠ADB= ![]() =
= ![]() ,
,
∴AD= ![]() =2
=2 ![]() .
.
【解析】(1)由平行线的性质和角平分线定义得出∠ABD=∠ADB,证出AB=AD,同理:AB=BC,得出AD=BC,证出四边形ABCD是平行四边形,即可得出结论;(2)由菱形的性质得出AC⊥BD,OD=OB= ![]() BD=3,再由三角函数即可得出AD的长.
BD=3,再由三角函数即可得出AD的长.


科目:初中数学 来源: 题型:
【题目】设中学生体质健康综合评定成绩为x分,满分为100分,规定:85≤x≤100为A级,75≤x≤85为B级,60≤x≤75为C级,x<60为D级.现随机抽取福海中学部分学生的综合评定成绩,整理绘制成如下两幅不完整的统计图,请根据图中的信息,解答下列问题:

(1)在这次调查中,一共抽取了 名学生,α= %;
(2)补全条形统计图;
(3)扇形统计图中C级对应的圆心角为 度;
(4)若该校共有2000名学生,请你估计该校D级学生有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,∠ABD、∠CDB的平分线BE、DF分别交边AD、BC于点E、F. 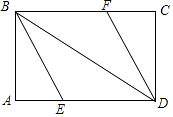
(1)求证:四边形BEDF是平行四边形;
(2)当∠ABE为多少度时,四边形BEDF是菱形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E、G分别是边AD、BC的中点,AF= ![]() AB.
AB.
(1)求证:EF⊥AG;
(2)若点F、G分别在射线AB、BC上同时向右、向上运动,点G运动速度是点F运动速度的2倍,EF⊥AG是否成立(只写结果,不需说明理由)?
(3)正方形ABCD的边长为4,P是正方形ABCD内一点,当S△PAB=S△OAB , 求△PAB周长的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:∠AOB和两点C、D,求作一点P,使PC=PD,且点P到∠AOB的两边的距离相等.(要求:用尺规作图,保留作图痕迹,不写作法,不要求证明)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一件工程甲独做50天可完,乙独做75天可完,现在两个人合作,但是中途乙因事离开几天,从开工后40天把这件工程做完,则乙中途离开了( )天.
A. 10 B. 20 C. 30 D. 25
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校“阳光足球俱乐部”计划购进一批甲、乙两种型号的足球,乙型足球每个进价比甲型足球每个进价多10元,若购进甲型足球3个和乙型足球5个,共需要资金370元.
(1)求甲、乙两种型号的足球进价各是多少元?
(2)该商店计划购进这两种型号的足球共50个,而可用于购买这两种型号的足球资金不少于2250元,但又不超过2270元.该商店有几种进货方案?
(3)已知商店出售一个甲种足球可获利6元,出售一个乙种足球可获利10元,试问在(2)的条件下,商店采用哪种方案可获利最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学新建了一栋7层的教学大楼,每层楼有8间教室,进出这栋大楼共有八道门,其中四道正门大小相同,四道侧门大小也相同.安全检查中,对八道门进行了测试:当同时开启一道正门和两道侧门时,2分内可以通过560名学生;当同时开启一道正门和一道侧门时,4分内可以通过800名学生.
(1)平均每分内一道正门和一道侧门分别可以通过多少名学生?
(2)检查中发现,紧急情况时因学生拥挤,出门的效率将降低30%.安全检查规定:在紧急情况下全大楼的学生应在5分内通过这八道门安全撤离,假设这栋教学大楼每间教室最多有45名学生,问建造的这八道门是否符合安全规定?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+c与x轴交于A,B两点,顶点为C,点P为抛物线上,且位于x轴下方.
(1)如图1,若P(1,﹣3),B(4,0).
①求该抛物线的解析式;
②若D是抛物线上一点,满足∠DPO=∠POB,求点D的坐标;
(2)如图2,已知直线PA,PB与y轴分别交于E、F两点.当点P运动时, ![]() 是否为定值?若是,试求出该定值;若不是,请说明理由.
是否为定值?若是,试求出该定值;若不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com