
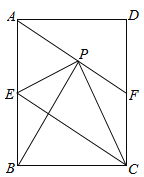
【题目】如图,在矩形ABCD中,E是AB边的中点,沿EC对折矩形ABCD,使B点落在点P处,折痕为EC,连结AP并延长AP交CD于F点,
(1)求证:四边形AECF为平行四边形;
(2)若△AEP是等边三角形,连结BP,求证:△APB≌△EPC;
(3)若矩形ABCD的边AB=6,BC=4,求△CPF的面积.
【答案】(1)证明见试题解析;(2)证明见试题解析;(3)![]() .
.
【解析】
试题分析:(1)由折叠的性质得到BE=PE,EC⊥PB,根据E为AB中点,得到AE=PE,利用等角对等边得到两对角相等,利用外角性质得到∠AEP=2∠EPB,设∠EPB=x,则∠AEP=2x,表示出∠APE,由∠APE+∠EPB得到∠APB为90°,进而得到AF与EC平行,再由AE与FC平行,利用两对边平行的四边形为平行四边形即可得证;
(2)根据等边三角形性质,得到△AEP三条边相等,三内角相等,再由折叠的性质及邻补角定义得到一对角相等,根据同角的余角相等得到一对角相等,再由AP=EB,利用AAS即可得证;
(3)过P作PM⊥CD,在Rt△EBC中,利用勾股定理求出EC,利用面积求出BQ,再根据BP=2BQ求出BP,在Rt△ABP中,利用勾股定理求出AP,根据AF-AP求出PF,由PM与AD平行,得到△PMF与△ADF相似,由相似得比例求出PM,再由FC=AE=3,求出△CPF面积即可.
试题解析:(1)由折叠得到BE=PE,EC⊥PB,∵E为AB的中点,∴AE=EB,即AE=PE,∴∠EBP=∠EPB,∠EAP=∠EPA,∵∠AEP为△EBP的外角,∴∠AEP=2∠EPB,设∠EPB=x,则∠AEP=2x,∠APE=![]() =90°﹣x,∴∠APB=∠APE+∠EPB=x+90°﹣x=90°,即BP⊥AF,∴AF∥EC,∵AE∥FC,∴四边形AECF为平行四边形;
=90°﹣x,∴∠APB=∠APE+∠EPB=x+90°﹣x=90°,即BP⊥AF,∴AF∥EC,∵AE∥FC,∴四边形AECF为平行四边形;
(2)∵△AEP为等边三角形,∴∠BAP=∠AEP=60°,AP=AE=EP=EB,∵∠PEC=∠BEC,∴∠PEC=∠BEC=60°,∵∠BAP+∠ABP=90°,∠ABP+∠BEQ=90°,∴∠BAP=∠BEQ,在△ABP和△EBC中,∵∠APB=∠EBC=90°,∠BAP=∠BEQ,AP=EB,∴△ABP≌△EBC(AAS),∵△EBC≌△EPC,∴△ABP≌△EPC;
(3)过P作PM⊥DC,交DC于点M,在Rt△EBC中,EB=3,BC=4,根据勾股定理得:EC=![]() =5,∵S△EBC=
=5,∵S△EBC=![]() EBBC=
EBBC=![]() ECBQ,∴BQ=
ECBQ,∴BQ=![]() =
=![]() ,由折叠得:BP=2BQ=
,由折叠得:BP=2BQ=![]() ,在Rt△ABP中,AB=6,BP=
,在Rt△ABP中,AB=6,BP=![]() ,根据勾股定理得:AP=
,根据勾股定理得:AP=![]() =
=![]() ,∵四边形AECF为平行四边形,∴AF=EC=5,FC=AE=3,∴PF=
,∵四边形AECF为平行四边形,∴AF=EC=5,FC=AE=3,∴PF=![]() =
=![]() ,∵PM∥AD,∴
,∵PM∥AD,∴![]() ,即
,即 ,解得:PM=
,解得:PM=![]() ,则S△PFC=
,则S△PFC=![]() FCPM=
FCPM=![]() =
=![]() .
.



科目:初中数学 来源: 题型:
【题目】如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是( ) 
A.12
B.24
C.12 ![]()
D.16 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,把△ABC向上平移3个单位长度,再向右平移2个单位长度,得到△A′B′C′.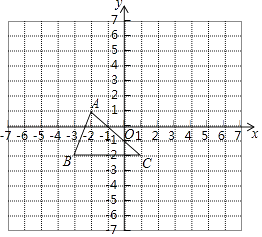
(1)在图中画出△A′B′C′;
(2)写出A′,B′的坐标;
(3)求三角形ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
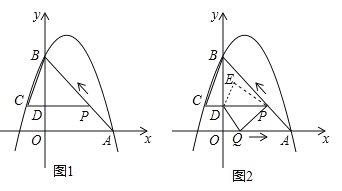
【题目】如图 1,二次函数![]() 的图像过点 A (3,0),B (0,4)两点,动点 P 从 A 出发,在线段 AB 上沿 A → B 的方向以每秒 2 个单位长度的速度运动,过点P作 PD⊥y 于点 D ,交抛物线于点 C .设运动时间为 t (秒).
的图像过点 A (3,0),B (0,4)两点,动点 P 从 A 出发,在线段 AB 上沿 A → B 的方向以每秒 2 个单位长度的速度运动,过点P作 PD⊥y 于点 D ,交抛物线于点 C .设运动时间为 t (秒).
(1)求二次函数![]() 的表达式;
的表达式;
(2)连接 BC ,当t=![]() 时,求△BCP的面积;
时,求△BCP的面积;
(3)如图 2,动点 P 从 A 出发时,动点 Q 同时从 O 出发,在线段 OA 上沿 O→A 的方向以 1个单位长度的速度运动,当点 P 与 B 重合时,P 、 Q 两点同时停止运动,连接 DQ 、 PQ ,将△DPQ沿直线 PC 折叠到 △DPE .在运动过程中,设 △DPE 和 △OAB重合部分的面积为 S ,直接写出 S 与 t 的函数关系式及 t 的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】底面半径为10cm,高为40cm的圆柱形水桶中装满了水。小明先将桶中的水倒满3个底面半径为3cm,高为5cm的圆柱形杯子,如果剩下的水倒在长、宽、高分别为50cm,20cm和12cm的长方体容器内,会满出来吗?若没有满出来,求出长方体容器内水的高度( ![]() 取3)。
取3)。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列计算正确的是( )
A.a4+a5=a9B.(2a2b3)2=4a4b6
C.﹣2a(a+3)=﹣2a2+6aD.(a+2b)2=4a2﹣b2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学课上,老师提出如下问题:
如图1,需要在A,B两地和公路l之间修地下管道,请你设计一种最节省材料的修建方案.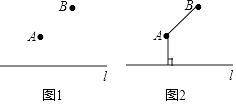
小军同学的作法如下:
①连接AB;
②过点A作AC⊥直线l于点C;
则折线段B﹣A﹣C为所求.
老师说:小军同学的方案是正确的.
请回答:该方案最节省材料的依据是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com