
【题目】底面半径为10cm,高为40cm的圆柱形水桶中装满了水。小明先将桶中的水倒满3个底面半径为3cm,高为5cm的圆柱形杯子,如果剩下的水倒在长、宽、高分别为50cm,20cm和12cm的长方体容器内,会满出来吗?若没有满出来,求出长方体容器内水的高度( ![]() 取3)。
取3)。
【答案】解:3×102×403×32×5×3=12000405=11595cm3.
长方体的容积为:50×20×12=12000cm3.
∵12000>11595,
∴不会满出来。
11595÷(50×20)=11.595cm.
∴长方体容器内水的高度11.595cm.
【解析】圆柱形的体积=底面积![]() 高,长方体的体积=长
高,长方体的体积=长![]() 宽
宽![]() 高。此题先求出剩下水的体积=圆柱形水桶的体积-3
高。此题先求出剩下水的体积=圆柱形水桶的体积-3![]() 圆柱形杯子的体积,及长方体的体积,再比较大小即可得出结论。
圆柱形杯子的体积,及长方体的体积,再比较大小即可得出结论。
【考点精析】通过灵活运用认识立体图形和有理数的四则混合运算,掌握有些几何图形的各个部分不都在同一平面内,它们是立体图形;在没有括号的不同级运算中,先算乘方再算乘除,最后算加减即可以解答此题.


科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C=90°,AC=3,AB=5,D为AB边上一点,DE∥AC,交BC于点E,DF∥BC,交AC于点F,连接EF,则线段EF的最小值为 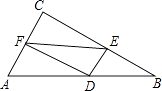
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D,E分别是AB,AC的中点,∠A=50°,∠ADE=60°,则∠C的度数为( ) 
A.50°
B.60°
C.70°
D.80°
查看答案和解析>>
科目:初中数学 来源: 题型:
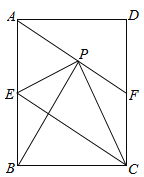
【题目】如图,在矩形ABCD中,E是AB边的中点,沿EC对折矩形ABCD,使B点落在点P处,折痕为EC,连结AP并延长AP交CD于F点,
(1)求证:四边形AECF为平行四边形;
(2)若△AEP是等边三角形,连结BP,求证:△APB≌△EPC;
(3)若矩形ABCD的边AB=6,BC=4,求△CPF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次数学活动课上,老师让同学们用两个大小、形状都相同的三角板画平行线AB,CD,并说出自己做法的依据.小琛、小萱、小冉三位同学的做法如下: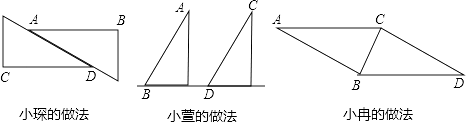
小琛说:“我的做法的依据是内错角相等,两直线平行.”
小萱做法的依据是 .
小冉做法的依据是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,并解决相关的问题.
按照一定顺序排列着的一列数称为数列,排在第一位的数称为第1项,记为a1 , 依此类推,排在第n位的数称为第n项,记为an .
一般地,如果一个数列从第二项起,每一项与它前一项的比等于同一个常数,那么这个数列叫做等比数列,这个常数叫做等比数列的公比,公比通常用字母q表示(q≠0).如:数列1,2,4,8,…为等比数列,其中a1=1,公比为q=2.
则:
(1)等比数列3,6,12,…的公比q为 , 第6项是 .
(2)如果一个数列a1 , a2 , a3 , a4 , …是等比数列,且公比为q,那么根据定义可得到: ![]() =q,
=q, ![]() =q,
=q, ![]() =q,…
=q,… ![]() =q.
=q.
所以:a2=a1q,a3=a2q=(a1q)q=a1q2 , a4=a3q=(a1q2)q=a1q3 , …
由此可得:an=(用a1和q的代数式表示).
(3)对等比数列1,2,4,…,2n﹣1求和,可采用如下方法进行:
设S=1+2+4+…+2n﹣1 ①,
则2S=2+4+…+2n ②,
②﹣①得:S=2n﹣1
利用上述方法计算:1+3+9+…+3n .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com