

分析 (1)根据全等三角形的性质即可求证△ACE≌△BCD,从而可知AE=BD;
(2)根据条件即可判断图中的全等直角三角形;
解答 解:(1)∵△ACB和△DCE都是等腰直角三角形,
∠ACB=∠DCE=90°,
∴AC=BC,DC=EC,
∴∠ACB+∠ACD=∠DCE+∠ACD,
∴∠BCD=∠ACE,
在△ACE与△BCD中,
$\left\{\begin{array}{l}{AC=BC}\\{∠ACE=∠BCD}\\{CE=CD}\end{array}\right.$
∴△ACE≌△BCD(SAS),
∴AE=BD,
(2)∵AC=DC,
∴AC=CD=EC=CB,
△ACB≌△DCE(SAS);
由(1)可知:∠AEC=∠BDC,∠EAC=∠DBC
∴∠DOM=90°,
∵∠AEC=∠CAE=∠CBD,
∴△EMC≌△BCN(ASA),
∴CM=CN,
∴DM=AN,
△AON≌△DOM(AAS),
∵DE=AB,AO=DO,
∴△AOB≌△DOE(HL)
点评 本题考查全等三角形,解题的关键是熟练运用全等三角形的判定条件,本题属于基础题型.


科目:初中数学 来源: 题型:选择题
| A. | y1<y2<y3 | B. | y2<y1<y3 | C. | y2<y3<y1 | D. | y1<y3<y2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
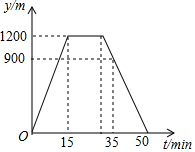 周日,小涛从家沿着一条笔直的公路步行去报亭看报,看了一段时间后,他按原路返回家中,小涛离家的距离y(单位:m)与他所用的时间t(单位:min)之间的函数关系如图所示,下列说法中正确的是( )
周日,小涛从家沿着一条笔直的公路步行去报亭看报,看了一段时间后,他按原路返回家中,小涛离家的距离y(单位:m)与他所用的时间t(单位:min)之间的函数关系如图所示,下列说法中正确的是( )| A. | 小涛家离报亭的距离是900m | |
| B. | 小涛从家去报亭的平均速度是60m/min | |
| C. | 小涛从报亭返回家中的平均速度是80m/min | |
| D. | 小涛在报亭看报用了15min |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 16个 | B. | 17个 | C. | 33个 | D. | 34个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
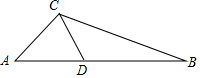 经过三边都不相等的三角形的一个顶点的线段把三角形分成两个小三角形,如果其中一个是等腰三角形,另外一个三角形和原三角形相似,那么把这条线段定义为原三角形的“和谐分割线”.如图,线段CD是△ABC的“和谐分割线”,△ACD为等腰三角形,△CBD和△ABC相似,∠A=46°,则∠ACB的度数为113°或92°.
经过三边都不相等的三角形的一个顶点的线段把三角形分成两个小三角形,如果其中一个是等腰三角形,另外一个三角形和原三角形相似,那么把这条线段定义为原三角形的“和谐分割线”.如图,线段CD是△ABC的“和谐分割线”,△ACD为等腰三角形,△CBD和△ABC相似,∠A=46°,则∠ACB的度数为113°或92°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com