
【题目】如图,△ABC中,AB=5,AC=8,BD,CD分别平分∠ABC,∠ACB,过点D作直线平行于BC,交AB,AC于E,F,则△AEF的周长为( )
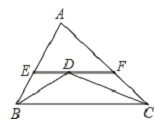
A.11B.13C.15D.18
【答案】B
【解析】
根据平行线的性质得到∠EDB=∠DBC,∠FDC=∠DCB,根据角平分线的性质得到∠EBD=∠DBC,∠FCD=∠DCB,等量代换得到∠EDB=∠EBD,∠FDC=∠FCD,于是得到ED=EB,FD=FC,即可得到结果.
解:∵EF∥BC,
∴∠EDB=∠DBC,∠FDC=∠DCB,
∵△ABC中,∠ABC和∠ACB的平分线相交于点D,
∴∠EBD=∠DBC,∠FCD=∠DCB,
∴∠EDB=∠EBD,∠FDC=∠FCD,
∴ED=EB,FD=FC,
∵AB=5,AC=8,
∴△AEF的周长为:AE+EF+AF=AE+ED+FD+AF=AE+EB+FC+AF=AB+AC=5+8=13.
故选:B.


科目:初中数学 来源: 题型:
【题目】已知:如图,在四边形ABCD中,AD∥BC,M为CD中点,AM平分∠DAB,AD+BC=AB.求证:BM平分∠ABC.

小淇证明过程如下:
延长BC至点F,使得CF=AD,连接MF.
∵ AD∥BC, ∴ ∠D=∠MCF.
∵ M为CD中点,∴ DM=CM.
在△ADM和△FCM中,

∴ △ADM≌△FCM(SAS). ∴ AM=FM.
∵ BF=BC+CF=BC+AD=AB,∴ △ABF是等腰三角形.
∴ BM平分∠ABC(等腰三角形底边上的中线与顶角的角平分重合).
(1)请你简要叙述小淇证明方法的错误之处;
(2)若AB=5,AM=3,求四边形ABCD面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2012年7月1日起,重庆实施阶梯电价,市民家庭每月用电量使用情况不同,按照用电量区间价格缴纳用电费用.其收费标准如下表:阶梯电价分三个档次.设某用户每月用电量为x度,应交电费为y元.
档次 | 用电量 | 每度电价格 |
第一档 | 不超过200度的部分 | 0.52元 |
第二档 | 超过200度不超过400度的部分 | 0.57元 |
第三档 | 超过400度的部分 | 0.82元 |
(1)直接写出y与x的关系式;
(2)小明家6、7月份共用电800度,应交电费471元,已知7月份的用电量比6月份的用电量大,求小明家6、7月份各用电多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在两个全等的等腰直角三角形ABC和EDC中,∠ACB=∠ECD=90°,点A与点E重合,点D与点B重合.现△ABC不动,把△EDC绕点C按顺时针方向旋转,旋转角为α(0°<α<90°).
(1)如图②,AB与CE交于点F,ED与AB,BC分别交于点M,H.求证:CF=CH;
(2)如图③,当α=45°时,试判断四边形ACDM的形状,并说明理由;
(3)如图②,在△EDC绕点C旋转的过程中,连结BD,当旋转角α的度数为多少时,△BDH是等腰三角形?



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八年级(1)班学生在完成课题学习“体质健康测试中的数据分析”后,利用课外活动时间积极参加体育锻炼,每位同学从篮球、跳绳、立定跳远、长跑、铅球中选一项进行训练,训练后都进行了测试.现将项目选择情况及训练后篮球定时定点投篮测试成绩整理后作出如下统计图.
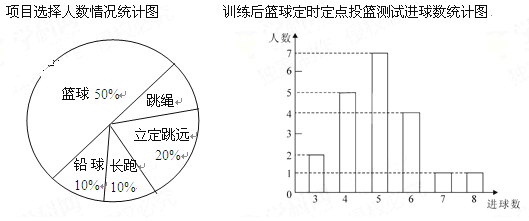
请你根据上面提供的信息回答下列问题:
(1)扇形图中跳绳部分的扇形圆心角为 度,该班共有学生 人, 训练后篮球定时定点投篮平均每个人的进球数是 .
(2)老师决定从选择铅球训练的3名男生和1名女生中任选两名学生先进行测试,请用列表或画树形图的方法求恰好选中两名男生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(初步探索)
截长补短法,是初中几何题中一种添加辅助线的方法,也是把几何题化难为易的一种策略.截长就是在长边上截取一条线段与某一短边相等,补短就是通过延长或旋转等方式使两条短边拼合到一起,从而解决问题.
(1)如图1,△ABC是等边三角形,点D是边BC下方一点,∠BDC=120°,探索线段DA、DB、DC之间的数量关系;

(灵活运用)
(2)如图2,△ABC为等边三角形,直线a∥AB,D为BC边上一点,∠ADE交直线a于点E,且∠ADE=60°.求证:CD+CE=CA;

(延伸拓展)
(3)如图3,在四边形ABCD中,∠ABC+∠ADC=180°,AB=AD.若点E在CB的延长线上,点F在CD的延长线上,满足EF=BE+FD,请直接写出∠EAF与∠DAB的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC≌△A′B′C,∠ACB=90°,∠B=50°,点B′在线段AB上,AC,A′B′交于点O,则∠COA′的度数是( )

A.50°B.60°
C.45°D.80°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请认真阅读下面的数学小探究系列,完成所提出的问题:
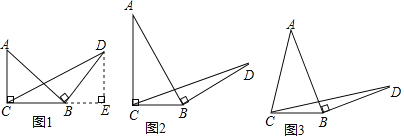
![]() 探究1:如图1,在等腰直角三角形ABC中,
探究1:如图1,在等腰直角三角形ABC中,![]() ,
,![]() ,将边AB绕点B顺时针旋转
,将边AB绕点B顺时针旋转![]() 得到线段BD,连接
得到线段BD,连接![]() 求证:
求证:![]() 的面积为
的面积为![]() 提示:过点D作BC边上的高DE,可证
提示:过点D作BC边上的高DE,可证![]() ≌
≌![]()
![]() 探究2:如图2,在一般的
探究2:如图2,在一般的![]() 中,
中,![]() ,
,![]() ,将边AB绕点B顺时针旋转
,将边AB绕点B顺时针旋转![]() 得到线段BD,连接
得到线段BD,连接![]() 请用含a的式子表示
请用含a的式子表示![]() 的面积,并说明理由.
的面积,并说明理由.
![]() 探究3:如图3,在等腰三角形ABC中,
探究3:如图3,在等腰三角形ABC中,![]() ,
,![]() ,将边AB绕点B顺时针旋转
,将边AB绕点B顺时针旋转![]() 得到线段BD,连接
得到线段BD,连接![]() 试探究用含a的式子表示
试探究用含a的式子表示![]() 的面积,要有探究过程.
的面积,要有探究过程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com