
����Ŀ��2012��7��1��������ʵʩ���ݵ�ۣ������ͥÿ���õ���ʹ�������ͬ�������õ�������۸�����õ���ã����շѱ����±������ݵ�۷��������Σ���ij�û�ÿ���õ���Ϊx�ȣ�Ӧ�����ΪyԪ��
���� | �õ��� | ÿ�ȵ�۸� |
��һ�� | ������200�ȵIJ��� | 0.52Ԫ |
�ڶ��� | ����200�Ȳ�����400�ȵIJ��� | 0.57Ԫ |
������ | ����400�ȵIJ��� | 0.82Ԫ |
��1��ֱ��д��y��x�Ĺ�ϵʽ��
��2��С����6��7�·ݹ��õ�800�ȣ�Ӧ�����471Ԫ����֪7�·ݵ��õ�����6�·ݵ��õ�������С����6��7�·ݸ��õ���ٶȣ�
���𰸡���1�� ����2��С����6�·��õ���Ϊ260�ȣ���7�·��õ���Ϊ540�ȣ�
����2��С����6�·��õ���Ϊ260�ȣ���7�·��õ���Ϊ540�ȣ�
��������
��1���ֶκ������ֱ����ÿһ�ε����������ɣ�
��2����6�·��õ���Ϊa,��7�·��õ���Ϊ(800-a),��������ȷ��a��ȡֵ��Χ���ٸ��ݷֶκ������۽�ɣ�
��1����0��x��200ʱ��y��0.52x��
��200��x��400ʱ��y��0.52��200+��x��200����0.57��0.57x��10��
��x��400ʱ��y��0.52��200+200��0.57+��x��400����0.82x��110��
����������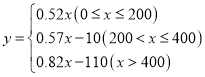 ��
��
��2����6�·��õ���Ϊa����7�·��õ���Ϊ��800��a����
��Ϊ7�·ݵ��õ�����6�·ݵ��õ���������a��800��a����a��400��
��0��x��200ʱ��800��a��400��
Ӧ�����Ϊ0.52a+0.82����800��a����110��471�����a��250��
��Ϊ250��200�����Բ��������⣬��ȥ��
��200��x��400ʱ��800��a��400��
Ӧ�����Ϊ0.57a��10+0.82����800��a����110��471�����a��260��
��Ϊ200��260��400ʱ�����Է���������800��a��800��260��540���ȣ���
����������С����6�·��õ���Ϊ260�ȣ���7�·��õ���Ϊ540�ȣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AB=AC=2����B=40������D���߶�BC���˶���D����B��C�غϣ�������AD������ADE=40����DE���߶�AC��E��

��1������BDA=115��ʱ����BAD= �㣻��D��B��C�˶�ʱ����BDA�� �����С������
��2����DC���ڶ���ʱ����ABD�ա�DCE����˵�����ɣ�
��3���ڵ�D���˶������У���ADE����״Ҳ�ڸı䣬�жϵ���BDA���ڶ��ٶ�ʱ����ADE�ǵ��������Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
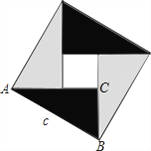
����Ŀ���й��Ŵ���ѧ���Ƕ��ڹ��ɶ����ķ��ֺ�֤������������ѧʷ�Ͼ��ж��صĹ��͵�λ����������ѧ�о��еļ̳кͷ�չ.����4��ȫ�ȵ�ֱ��������ƴ����ͼ��ʾ����ͼ��.Rt��ABC�У���ACB=90�㣬��![]() �������������ͼ�ν���������⣺
�������������ͼ�ν���������⣺
��1����˵��![]() ��
��
��2������������ε������10��С�����ε������2����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���![]() ��a��0����ͼ����ͼ��ʾ����������������ȷ���ǣ�������
��a��0����ͼ����ͼ��ʾ����������������ȷ���ǣ�������

A. a ��b��c
B. һ�κ���y=ax +c��ͼ����������
C. m��am+b��+b��a��m������ʵ����
D. 3b+2c��0
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У���BAD=130������B=��D=90������BC��CD�Ϸֱ���һ��M��N��ʹ������AMN�ܳ���Сʱ�����MAN�Ķ���Ϊ_________.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,��֪��ABC��,��B=90����AB=8��CB=6��P��Q����ABC���ϵ���������,���е�P�ӵ�A��ʼ��A��B�����˶�,���ٶ�Ϊÿ��1cm,��Q�ӵ�B��ʼ��B��C�����˶�,���ٶ�Ϊÿ��2cm,����ͬʱ����,�������ʱ��Ϊt��.

(1)��t=2��ʱ,��PQ�ij�;
(2)�����ʱ��Ϊ����ʱ,��PQB�ǵ���������?
(3)��Q��B��C��A�����˶�,��Q�ڱ�CA���˶�ʱ,����ʹ��BCQ��Ϊ���������ε��˶�ʱ�䡣
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,ֱ��y=![]() x+2�ֱ���x�ᡢy���ཻ�ڵ�A����B
x+2�ֱ���x�ᡢy���ཻ�ڵ�A����B

��1�����A�͵�B�����ꣻ
��2������P��y���ϵ�һ�㣬����AOB����ABP������ֱ�ΪS��AOB��S��ABP����S��ABP=2S��AOB�����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�AB��5��AC��8��BD��CD�ֱ�ƽ�֡�ABC����ACB������D��ֱ��ƽ����BC����AB��AC��E��F������AEF���ܳ�Ϊ��������
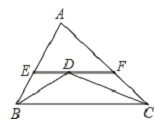
A.11B.13C.15D.18
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��CA=CB��CD=CE����ACB=��DCE=����
��1����֤��BE=AD��

��2������=90��ʱ��ȡAD��BE���е�ֱ�Ϊ��P��Q������CP��CQ��PQ����ͼ�ڣ��ж���CPQ����״��������֤����

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com