
【题目】阅读材料:
在数轴上,点 A 在原点 0 的左边,距离原点 4 个单位长度,点 B 在原点的右边,点 A 和点 B 之间的距离为 14个单位长度.
(1)点 A 表示的数是 ,点 B 表示的数是 ;
(2)点 A、B 同时出发沿数轴向左移动,速度分别为 1 个单位长度/秒,3 个单位长度/秒,经过多少秒,点 A 与点 B重合?
(3)点 M、N 分别从点 A、B 出发沿数轴向右移动,速度分别为 1 个单位长度/秒、2 个单位长度/秒,点 P 为 ON 的中点,设 OP-AM 的值为 y,在移动过程中,y 值是否发生变化?若不变,求出 y 值;若变化,说明理由.
【答案】(1)-4,10(2)7秒(3)不变化,理由详解解析
【解析】
(1)由A在原点左边4个单位长度可知A点表示的数是-4,再根据B 在原点右边且与点A距离14个单位长度,可由-4+14=10可得B点表示的数.
(2)把A,B看成距离为14个单位长度的追击问题,由速度差×相遇时间=相距距离列出等式求解.
(3)设移动时间为x秒,用含有x的代数式表示出OP与AM的长度,然后根据y= OP-AM列出关系式判断,若式中不含x项则不发生变化,含x项则发生变化.
(1)由A在原点左边4个单位长度可知A点表示的数是-4,由B 在原点右边且与点A距离14个单位长度可知,-4+14=10,则B点表示的数是10.
(2)由题意知,此时为速度问题里面的追击问题,则由速度差×相遇时间=相距距离可知:
设经过x秒后重合,即x秒后AB相遇.
则(3-1)x=14
解得:x=7
故7秒后点A,B重合.
(3)y不发生变化,理由如下:
设运动时间为x秒,则AM=x
而OP=![]()
则y=OP-AM=![]()
故y为定值,不发生变化.


科目:初中数学 来源: 题型:
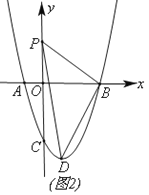
【题目】如图,在平面直角坐标中,抛物线y=ax2-2ax-3a(a≠0)与x轴交于A、B(A在B的左侧),与y轴交于点C,且OC=3OA.
(1)如图(1)求抛物线的解析式;
(2)如图(2)动点P从点O出发,沿y轴正方向以每秒1个单位的速度移动,点D是抛物线顶点,连接PB、PD、BD,设点P运动时间为t(单位:秒),△PBD的面积为S,求S与t的函数关系式;
(3)如图(3)在(2)的条件下,延长BP交抛物线于点Q,过点O作OE⊥BQ,垂足为E,连接CE、CB,若CE=CB,求t值,并求出此时的Q点坐标.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司招聘一名员工,现有甲、乙两人竞聘,公司聘请了3位专家和4位群众代表组成评审组,评审组对两人竟聘演讲进行现场打分,记分采用100分制,其得分如下表:
评委(序号) | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
甲(得分) | 89 | 94 | 93 | 87 | 95 | 92 | 87 |
乙(得分) | 87 | 89 | 91 | 95 | 94 | 96 | 89 |
(1)甲、乙两位竞聘者得分的中位数分别是多少
(2)计算甲、乙两位应聘者平均得分,从平均得分看应该录用谁(结果保留一位小数)
(3)现知道1、2、3号评委为专家评委,4、5、6、7号评委为群众评委,如果对专家评委组与群众评委组的平均分数分别赋子适当的权,那么对专家评委组赋的权至少为多少时,甲的平均得分比乙的平均得分多0.5分及以上
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数![]() 的图象经过第四象限的点B(3,a),且与x轴相交于原点和点A(7,0)
的图象经过第四象限的点B(3,a),且与x轴相交于原点和点A(7,0)
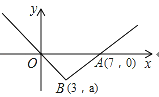
(1)求k、b的值;
(2)当x为何值时,y>﹣2;
(3)点C是坐标轴上的点,如果△ABC恰好是以AB为腰的等腰三角形,直接写出满足条件的点C的坐标
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在解决问题:已知a=![]() ,求2a2﹣8a+1的值,他是这样分析与解的:
,求2a2﹣8a+1的值,他是这样分析与解的:
∵a=![]() =
=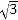 =2﹣
=2﹣![]()
∴a﹣2=﹣![]()
∴(a﹣2)2=3,a2﹣4a+4=3
∴a2﹣4a=﹣1
∴2a2﹣8a+1=2(a2﹣4a)+1=2×(﹣1)+1=﹣1
请你根据小明的分析过程,解决如下问题:
(1)化简![]() +
+![]() +
+![]() +…+
+…+![]()
(2)若a=![]() ,求4a2﹣8a+1的值.
,求4a2﹣8a+1的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在以O为原点的直角坐标系中,抛物线的顶点为A (﹣1,﹣4),且经过点B(﹣2,﹣3),与x轴分别交于C、D两点.
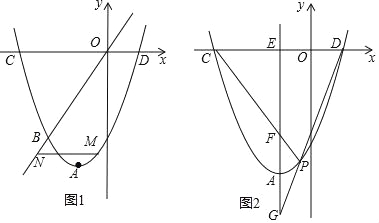
(1)求直线OB以及该抛物线相应的函数表达式;
(2)如图1,点M是抛物线上的一个动点,且在直线OB的下方,过点M作x轴的平行线与直线OB交于点N,求MN的最大值;
(3)如图2,过点A的直线交x轴于点E,且AE∥y轴,点P是抛物线上A、D之间的一个动点,直线PC、PD与AE分别交于F、G两点.当点P运动时,EF+EG是否为定值?若是,试求出该定值;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线EF交AC于点E,交BC于点F.试探索BF与CF的数量关系,写出你的结论并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B、C三瓶不同浓度的酒精,A瓶内有酒精2kg,浓度x%,B瓶有酒精3kg,浓度y%,C瓶有酒精5kg,浓度z%,从A瓶中倒出10%,B瓶中倒出20%,C瓶中倒出24%,混合后测得浓度33.5%,将混合后的溶液倒回瓶中,使它们恢复原来的质量,再从A瓶倒出30%,B瓶倒出30%,C瓶倒出30%,混合后测得浓度为31.5%,测量发现![]() ,
,![]() ,
,![]() ,且x、y、z均为整数,则把起初A、B两瓶酒精全部混合后的浓度为______.
,且x、y、z均为整数,则把起初A、B两瓶酒精全部混合后的浓度为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有理数a、b、c在数轴上的位置如图所示:
![]()
(1)用“>”、“=”或“<”填空:︱b︱ ︱c︱;—a c.
(2)化简:|b-c|-|b-a|+|a+c|.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com