
【题目】某公交公司有 A,B 型两种客车,它们的载客量和租金如下表:
A | B | |
载客量(人/辆) | 45 | 30 |
租金(元/辆) | 400 | 280 |
红星中学根据实际情况,计划租用 A,B 型客车共 5 辆,同时送七年级师生到基地参加社会实践活动,设租用 A 型客车 x 辆,根据要求回答下列问题:
(1)用含 x 的式子填写下表:
车辆数(辆) | 载客量 | 租金(元) | |
A | x | ||
B |
(2)若要保证租车费用不超过 1 900 元,求 x 的最大值.
【答案】(1)表格见解析
(2)4
【解析】
(1)根据载客量和租金表,且载客量=汽车辆数![]() 单车载客量,租金=汽车辆数
单车载客量,租金=汽车辆数![]() 单车租金列出代数表达式填入表中即可.
单车租金列出代数表达式填入表中即可.
(2)根据题意表示出租车总费用,列出不等式即可解决;
此题主要考查了一次不等式的综合应用,由题意得出租用x辆甲种客车与总租金关系是解决问题的关键.
(1)∵载客量=汽车辆数×单车载客量,租金=汽车辆数×单车租金,
∴B型客车载客量=30(5x);B型客车租金=280(5x);
填表如下:
车辆数(辆) | 载客量 | 租金(元) | |
A | x | 45 x | 400 x |
B | 5-x | 30(5-x) | 280(5-x) |
(2)根据题意得
400x+280(5x)1900
400x+1400-280x1900
120x500
x![]()
∴x的最大值为4;


科目:初中数学 来源: 题型:
【题目】如图,BC是⊙O的直径,AD是⊙O的切线,切点为D,AD与CB的延长线交于点A,∠C=30°,给出下面四个结论:①AD=DC;②AB=BD;③AB=![]() BC;④BD=CD,
BC;④BD=CD,
其中正确的个数为( )

A. 4个B. 3个C. 2个D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
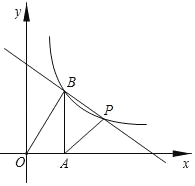
【题目】如图,在平面直角坐标系中,函数y=![]() 的图象经过点P(4,3)和点B(m,n)(其中0<m<4),作BA⊥x轴于点A,连接PA,PB,OB,已知S△AOB=S△PAB.
的图象经过点P(4,3)和点B(m,n)(其中0<m<4),作BA⊥x轴于点A,连接PA,PB,OB,已知S△AOB=S△PAB.
(1)求k的值和点B的坐标.
(2)求直线BP的解析式.
(3)直接写出在第一象限内,使反比例函数大于一次函数的x的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
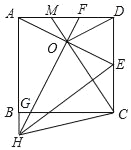
【题目】如图,正方形ABCD中,E为CD的中点,AE的垂直平分线分别交AD,BC及AB的延长线于点F,G,H,连接HE,HC,OD,连接CO并延长交AD于点M.则下列结论中:
①FG=2AO;②OD∥HE;③![]() ;④2OE2=AHDE;⑤GO+BH=HC
;④2OE2=AHDE;⑤GO+BH=HC
正确结论的个数有( )
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
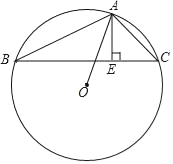
【题目】如图,在钝角△ABC中,∠C=45°,AE⊥BC,垂足为E点,且AB与AC的长度为方程x2﹣9x+18=0的两个根,⊙O是△ABC的外接圆.
求:(1)⊙O的半径;
(2)BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△OAB中,OA=OB=10cm,∠AOB=80°,以点O为圆心,半径为6cm的优弧弧MN分别交OA,OB于点M,N.
(1)点P在右半弧上(∠BOP是锐角),将OP绕点O逆时针旋转80°得OP′.求证:AP=BP′;
(2)点T在左半弧上,若AT与弧相切,求AT的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,AC是对角线,今有较大的直角三角板,一边始终经过点B,直角顶点P在射线AC上移动,另一边交DC于点Q.
(1)如图①,当点Q在DC边上时,猜想并写出PB与PQ所满足的数量关系,并加以证明;
(2)如图②,当点Q落在DC的延长线上时,猜想并写出PB与PQ满足的数量关系,并证明你的猜想.

查看答案和解析>>
科目:初中数学 来源: 题型:
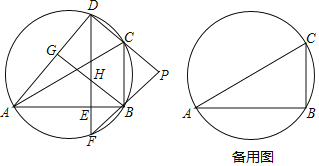
【题目】如图,D是△ABC外接圆上的动点,且B,D位于AC的两侧,DE⊥AB,垂足为E,DE的延长线交此圆于点F.BG⊥AD,垂足为G,BG交DE于点H,DC,FB的延长线交于点P,且PC=PB.
(1)求证:BG∥CD;
(2)设△ABC外接圆的圆心为O,若AB=![]() DH,∠OHD=80°,求∠BDE的大小.
DH,∠OHD=80°,求∠BDE的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com