
【题目】如图,A(6, 0),B(0, 4),点B关于x轴的对称点为C点,点D在x轴的负半轴上,△ABD的面积是30.
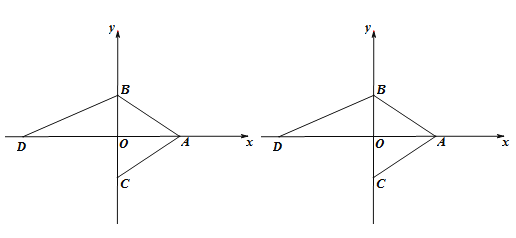
(1)求点D坐标.
(2)若动点P从点B出发,沿射线BC运动,速度为每秒1个单位,设P的运动时间为t秒,△APC的面积为S,求S与t的关系式.
(3)在(2)的条件下,同时点Q从D点出发沿x轴正方向以每秒2个单位速度匀速运动,若点R在过A点且平行于y轴的直线上,当△PQR为以PQ为直角边的等腰直角三角形时,求满足条件的t值,并直接写出点R的坐标.
【答案】(1)(-9,0);(2)当0<t≤8时,S=![]() ×(8-t)×6=-3t+24;当t>8时,S=
×(8-t)×6=-3t+24;当t>8时,S=![]() ×(t-8)×6=3t-24;(3)t=10秒或11秒或17秒时,△PQR是等腰直角三角形.
×(t-8)×6=3t-24;(3)t=10秒或11秒或17秒时,△PQR是等腰直角三角形.
【解析】
(1)根据三角形面积公式求出AD即可.
(2)分两种情形①当0<t≤8时,②当t>8时,求出△PAC面积即可.
(3)分三种情形①如图1中,当∠QPR=90°,PQ=PR时,作RH⊥OP于H,②如图2中,当∠PQR=90°,QR=PQ时,③如图3中,当∠QRP=90°,QR=PR,利用全等三角形的性质列出方程即可解决.
解:(1)∵A(6,0),B(0,4),△ABD的面积是30,
∴![]() ADBO=30,
ADBO=30,
∴![]() AD4=30,
AD4=30,
∴AD=15,
∴OD=9,
∴点D坐标为(-9,0).
(2)∵点B(0,4)关于x轴的对称点为C点,
∴点C坐标(0,-4),
∴当0<t≤8时,S=![]() ×(8-t)×6=-3t+24,
×(8-t)×6=-3t+24,
当t>8时,S=![]() ×(t-8)×6=3t-24.
×(t-8)×6=3t-24.
(3)①如图1中,
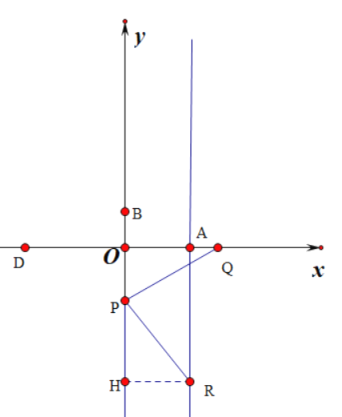
图1
当∠QPR=90°,PQ=PR时,作RH⊥OP于H,
∵∠QPO+∠RPH=90°,∠QPO+∠PQO=90°,
∴∠PQO=∠RPH,
在△PQO和△RPH中,
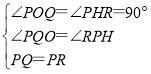
∴△PQO≌RPH,
∴RH=PO,
∵四边形AOHR是矩形,
∴RH=AO=6,
∴OP=6,
∴t-4=6,
∴t=10.
②如图2中,
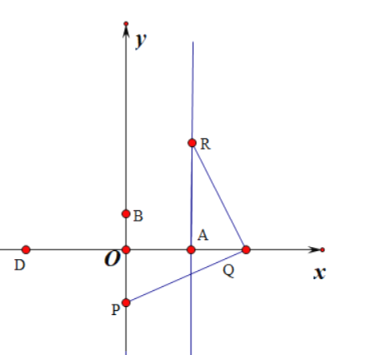
图2
当∠PQR=90°,QR=PQ时,
∵∠RQA+∠OQP=90°,∠OQP+∠OPQ=90°,
∴∠RQA=∠OPQ,
在△ARQ和△OQP中,
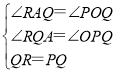
∴△ARQ≌△OQP,
∴OP=AQ,
∴t-4=2t-15,
∴t=11.
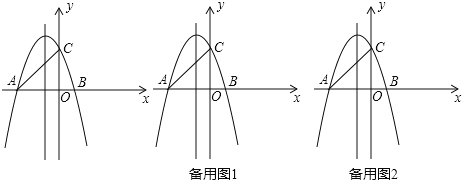
③如图3中,
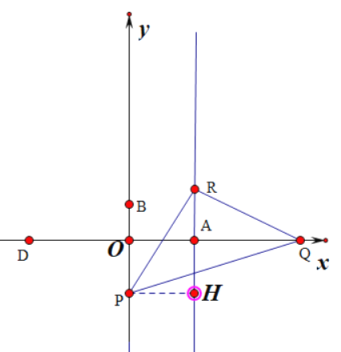
图3
当∠QRP=90°,QR=PR,
∵∠RQA+∠PRH=90°,∠PRH+∠RPH=90°,/span>
∴∠QRA=∠RPH,
在△AQR和△HRP中,
∠QRA=∠RPH |
∠QAR=∠RHP |
QR=PR |
∴△AQR≌△HRP,
∴AQ=RH,AR=PH=AO=6,
∴OP=AH=RH-AR=AQ-AR=AQ-6
∴t-4=2t-15-6,
∴t=17.
综上所述t=10秒或11秒或17秒时,△PQR是等腰直角三角形.


 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=x+3分别交x轴、y轴于A,C两点,抛物线y=ax2+bx+c(a≠0),经过A,C两点,与x轴交于点B(1,0).
(1)求抛物线的解析式;
(2)点D为直线AC上一点,点E为抛物线上一点,且D,E两点的横坐标都为2,点F为x轴上的点,若四边形ADEF是平行四边形,请直接写出点F的坐标;
(3)若点P是线段AC上的一个动点,过点P作x轴的垂线,交抛物线于点Q,连接AQ,CQ,求△ACQ的面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知DE∥BC,BE平分∠ABC,∠C=65°,∠ABC=50°.
(1)求∠BED的度数;
(2)判断BE与AC的位置关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD⊥BC于D,BD=AD,DG=DC,E,F分别是BG,AC的中点.
(1)求证:DE=DF,DE⊥DF;
(2)连接EF,若AC=10,求EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】教材中的探究:如图1,把两个边长为1的小正方形沿对角线剪开,所得的4个直角三角形拼成一个面积为2的大正方形.由此,得到了一种能在数轴上画出无理数对应点的方法.
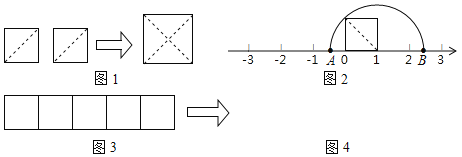
(1)图2中A、B两点表示的数分别为 , ;
(2)请你参照上面的方法,把长为5,宽为1的长方形进行裁剪,拼成一个正方形.
①在图3中画出裁剪线,并在图4位置画出所拼正方形的示意图.
②在数轴上分别标出表示数![]() 以及
以及![]() ﹣3的点,(图中标出必要线段长)
﹣3的点,(图中标出必要线段长)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在锐角△ABC中,∠A=60°,∠ACB=45°,以BC为弦作⊙O,交AC于点D,OD与BC交于点E,若AB与⊙O相切,则下列结论:
①∠BOD=90°;②DO∥AB;③CD=AD;④△BDE∽△BCD;⑤![]()
正确的有( )
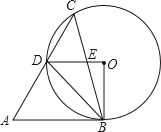
A. ①② B. ①④⑤ C. ①②④⑤ D. ①②③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面上有四个点A,B,C,D.
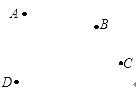
(1)根据下列语句画图:
①射线BA;
②直线AD,BC相交于点E;
③延长DC至F(虚线),使CF=BC,连接EF(虚线).
(2)图中以E为顶点的角中,小于平角的角共有__________个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王先生到市行政中心大楼办事,假定乘电梯向上一楼记作+1,向下一楼记作-1,王先生从1楼出发,电梯上下楼层依次记录如下(单位:层):![]() .
.
(1)请你通过计算说明王先生最后是否回到出发点![]() 楼.
楼.
(2)该中心大楼每层高3m,电梯每向上或下1m需要耗电0.3度,根据王先生现在所处位置,请你算算,他办事时电梯需要耗电多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解市民私家车出行的情况,某市交通管理部门对拥有私家车的市民进行随机抽样调查、其中一个问题是“你平均每天开车出行的时间是多少”共有4个选项:A、1小时以上(不含1小时);B:0.5-1小时(不含0.5小时);C:0-0.5小时(不含0小时);D,不开车.图1、2是根据调査结果绘制的两幅不完整的统计图,请你根据统计图提供的信息,解答以下问题:
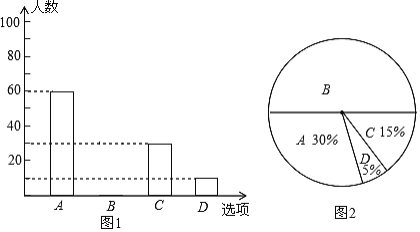
(1)本次一共调查了______名市民;
(2)在图1中将选项B的部分补充完整,并求图2中,A类所对应扇形圆心角α的度数;
(3)若该市共有200万私家车,你估计全市可能有多少私家车平均每天开车出行的时间在1小时以上?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com