
【题目】定义:有一组对角互补的凸四边形叫做“对补四边形”,性质:“对补四边形”一定是圆内接四边形.
(1)概念理解:请你根据上述描述定义举一个“对补四边形”的例子;
(2)问题探究:如图1,在对补四边形ABCD中,如果∠A=∠C,试探究AB、AD、BC、CD之间的数量关系,并说明理由;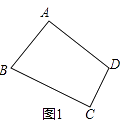
(3)应用拓展:如图2,在四边形ABCD中,AB≠BC,∠A=∠C=90°,连接BD,将△BCD沿BD折叠,得到△BFD.
①连接AF,四边形ABDF是对补四边形吗?请说明理由;
②若AB=1,BD=2,且BF把△ABD分成两个三角形的面积比为1:2,请求出CD的长.
【答案】
(1)解:矩形是“对补四边形”
(2)解:AB2+AD2=BC2+CD2;理由如下:
连接BD,如图1所示:
∵四边形ABCD是“对补四边形”,
∴∠A=+∠C=90°,
∵∠A=∠C,
∴∠A=∠C=90°,
∴AB2+AD2=BD2,BC2+CD2=BD2,
∴AB2+AD2=BC2+CD2
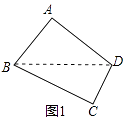
(3)解:①四边形ABDF是对补四边形,理由如下:
∵∠BAD=∠C=90°,
∴∠BAD+∠C=180°,
∴A、B、C、D四点共圆,
由折叠的性质得:∠BFD=∠BAD=90°,
∴点F在A、B、C、D四点共圆的这个圆上,
∴∠BAF+∠BDF=180°,
∴四边形ABDF是对补四边形;
②∵AB=1,BD=2,∠BAD=90°,
∴sin∠ADB= ![]() =
= ![]() ,AD=
,AD= ![]() =
= ![]() ,
,
∴∠ADB=30°,
∴∠ABD=60°,
设AD与BF交于点P,作PM⊥BD于M,如图2所示:
∵BF把△ABD分成两个三角形的面积比为1:2,
∴AP:PD=1:2,或PD:AP=1:2,
,当AP:PD=1:2时,AP= ![]() AD=
AD= ![]() ,PD=
,PD= ![]() AD=
AD= ![]() ,
,
∴∠ADB=30°,
∴PM= ![]() PD=
PD= ![]() =PA,
=PA,
∴∠ABP=∠DBP= ![]() ∠ABD=30°,
∠ABD=30°,
∵∠BFD=90°,
∴DF= ![]() BD=1,
BD=1,
∴CD=DF=1;
当PD:AP=1:2时,PD= ![]() AD=
AD= ![]() ,AP=
,AP= ![]() AD=
AD= ![]() ,
,
∴BP= ![]() =
= ![]() ,
,
∵∠BAD=∠BFD=90°,∠APB=∠FPD,
∴△ABP∽△FDP,
∴ ![]() ,即
,即  ,
,
解得:FD= ![]() ,
,
∴CD=FD= ![]() ;
;
综上所述:CD的长为1或 ![]() .
.
【解析】(1)由矩形的性质容易得出矩形是“对补四边形”
(2)连接BD,由“对补四边形”的定义得出∠A=+∠C=90°,由已知得出∠A=∠C=90°,由勾股定理得出AB2+AD2=BD2,BC2+CD2=BD2,即可得出结论;
(3)①证明A、B、C、D四点共圆,由折叠的性质得:∠BFD=∠BAD=90°,证出点F在A、B、C、D四点共圆的这个圆上,由圆内接四边形的性质得出∠BAF+∠BDF=180°,即可得出结论;②由三角函数得出sin∠ADB= ![]() =
= ![]() ,由勾股定理求出AD=
,由勾股定理求出AD= ![]() =
= ![]() ,得出∠ADB=30°,由直角三角形的性质得出∠ABD=60°,设AD与BF交于点P,作PM⊥BD于M,由已知得出AP:PD=1:2,或PD:AP=1:2,分别求出DF的长,即可得出CD的长.
,得出∠ADB=30°,由直角三角形的性质得出∠ABD=60°,设AD与BF交于点P,作PM⊥BD于M,由已知得出AP:PD=1:2,或PD:AP=1:2,分别求出DF的长,即可得出CD的长.
【考点精析】认真审题,首先需要了解相似三角形的应用(测高:测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决;测距:测量不能到达两点间的举例,常构造相似三角形求解).


 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:初中数学 来源: 题型:
【题目】某市为提倡节约用水,准备实行自来水“阶梯计费”方式,用户用水不超出基本用水量的部分享受基本价格,超出基本用水量的部分实行加价收费,为更好地做决策,自来水公司随机抽取部分用户的用水量数据,并绘制了如图不完整的统计图(每组数据包括右端点但不包括左端点),请你根据统计图解决下列问题:
(1)此次抽样调查的样本容量是 .
(2)补全频数分布直方图.
(3)如果自来水公司将基本用水量定为每户25吨,那么该地区6万用户中约有多少用户的用水全部享受基本价格?
查看答案和解析>>
科目:初中数学 来源: 题型:
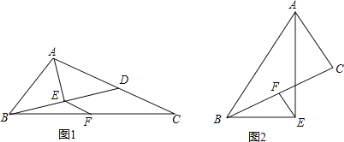
【题目】如图,在△ABC中,AE平分∠BAC,BE⊥AE于点E,点F是BC的中点.
(1)如图1,BE的延长线与AC边相交于点D,求证:EF=![]() (AC﹣AB);
(AC﹣AB);
(2)如图2,请直接写出线段AB、AC、EF之间的数量关系。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,ABCD 中,∠ABC、∠ADC的平分线分别交AD、BC于点E、F.
(1)求证:四边形EBFD是平行四边形;
(2)小明在完成(1)的证明后继续进行了探索.连接AF、CE,分别交BE、FD于点G、H,得到四边形EGFH.此时,他猜想四边形EGFH是平行四边形,请在框图(图2)中补全他的证明思路.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将点A先向右平移3个单位长度,在向下平移5个单位长度,得到A’;将点B先向下平移5个单位长度,再向右平移4个单位长度,得到B’,则A’与B’相距( )

A. 4个单位长度 B. 5个单位长度 C. 6个单位长度 D. 7个单位长度
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过原点O的直线与双曲线y= ![]() 交于A、B两点,过点B作BC⊥x轴,垂足为C,连接AC,若S△ABC=5,则k的值是( )
交于A、B两点,过点B作BC⊥x轴,垂足为C,连接AC,若S△ABC=5,则k的值是( ) 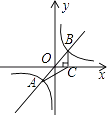
A.![]()
B.![]()
C.5
D.10
查看答案和解析>>
科目:初中数学 来源: 题型:
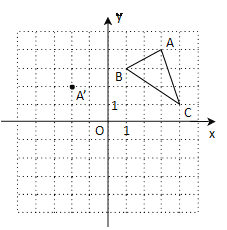
【题目】在平面直角坐标系中,三角形ABC的三个顶点的位置如图所示,点A/的坐标是(—2,2),现将三角形ABC平移,使点A平移到A/,点B/、C/分别是B、C的对应点.
(1)请画出平移后的三角形A/B/C/,并直接写出点B/、C/的坐标;
(2)若三角形ABC内部一点P的坐标为(a,b),则点P的对应点P/的坐标是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCF中,∠ACB=90°,点E是AB边的中点,点F恰是点E关于AC所在直线的对称点.
(1)证明:四边形CFAE为菱形;
(2)连接EF交AC于点O,若BC=10,求线段OF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,点A、B的坐标分别为(1,5)和(4,0),点C是y轴上的一个动点,且A、B、C三点不再同一条直线上,当△ABC的周长最小时,点C的坐标是( )
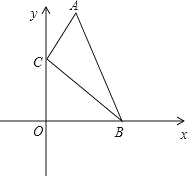
A. (0,1) B. (0,2) C. (0,3) D. (0,4)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com