
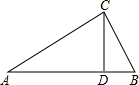
 如图,在Rt△ABC中,∠C=90°,CD是斜边AB上的高.
如图,在Rt△ABC中,∠C=90°,CD是斜边AB上的高.分析 (1)求出∠CDA=∠ACB=90°,根据有两个角对应相等的两三角形相似得出△ACD∽△ABC,△CBD∽△ABC,即可得出答案;
(2)根据相似三角形的性质得到比例式,由比例式得到等积式,结论即可得到;
(3)根据三角形相似得到比例式,由比例式化成等积式即可.
解答 (1)证明:∵∠ACB=90°,CD⊥AB,
∴∠CDA=∠ACB=90°,
∵∠A=∠A,
∴△ACD∽△ABC,
同理△CBD∽△ABC,
∴△ACD∽△CBD∽ABC;
(2)∵△ABC∽△ACD,∴$\frac{AB}{AC}$=$\frac{AC}{AD}$,
∴AC2=AB•AD,
∴AC是AB,AD的比例中项,
故答案为:AB,AD;
(3)∵△CBD∽△ABC,
∴$\frac{BC}{AB}=\frac{BD}{BC}$,
∴BC2=AB•BD,
∵△ACD∽△BCD,
∴$\frac{CD}{BD}=\frac{AD}{CD}$,
∴CD2=AD•BD.
点评 本题考查了相似三角形的判定和性质,有关比例中项问题,熟练掌握相似三角形的判定和性质定理是解题的关键.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}+\sqrt{3}$=$\sqrt{5}$ | B. | 3$\sqrt{2}$-$\sqrt{2}$=3 | C. | $\sqrt{2}×\sqrt{5}$=$\sqrt{10}$ | D. | $\frac{\sqrt{2}}{\sqrt{5}}$=5$\sqrt{10}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
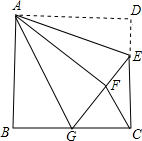 如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.下列结论:①△ABG≌△AFG;②BG=GC;③AG∥CF;④△GCF是等边三角形;⑤S△CFG=$\frac{18}{5}$.其中正确的结论是①②③⑤.(只填序号).
如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.下列结论:①△ABG≌△AFG;②BG=GC;③AG∥CF;④△GCF是等边三角形;⑤S△CFG=$\frac{18}{5}$.其中正确的结论是①②③⑤.(只填序号).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
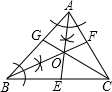 如图,AE于BF交于点O,点O在CG上,根据尺规作图的痕迹,判断下列说法不正确的是( )
如图,AE于BF交于点O,点O在CG上,根据尺规作图的痕迹,判断下列说法不正确的是( )| A. | AE、BF是△ABC的内角平分线 | B. | 点O到△ABC三边的距离相等 | ||
| C. | CG也是△ABC的一条内角平分线 | D. | AO=BO=CO |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
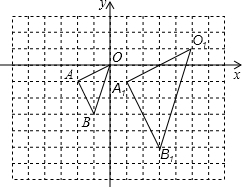 在如图的方格中,△OAB的顶点坐标分别为O(0,0)、A(-2,-1)、B(-1,-3),△O1A1B1与△OAB是关于点P为位似中心的位似图形.
在如图的方格中,△OAB的顶点坐标分别为O(0,0)、A(-2,-1)、B(-1,-3),△O1A1B1与△OAB是关于点P为位似中心的位似图形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
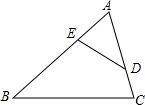 如图,在△ABC中,∠B+∠CDE=∠C+∠BED,AE=2,AD=3,CD=1,则BE等于( )
如图,在△ABC中,∠B+∠CDE=∠C+∠BED,AE=2,AD=3,CD=1,则BE等于( )| A. | $\frac{3}{2}$ | B. | $\frac{2}{3}$ | C. | 2 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com