
【题目】如图,在Rt△ABC中,∠C=90°,CA=12 ![]() cm,BC=12cm;动点P从点C开始沿CA以2
cm,BC=12cm;动点P从点C开始沿CA以2 ![]() cm/s的速度向点A移动,动点Q从点A开始沿AB以4cm/s的速度向点B移动,动点R从点B开始沿BC以 2cm/s的速度向点C移动.如果P、Q、R分别从C、A、B同时移动,移动时间为t(0<t<6)s.
cm/s的速度向点A移动,动点Q从点A开始沿AB以4cm/s的速度向点B移动,动点R从点B开始沿BC以 2cm/s的速度向点C移动.如果P、Q、R分别从C、A、B同时移动,移动时间为t(0<t<6)s.
(1)∠CAB的度数是;
(2)以CB为直径的⊙O与AB交于点M,当t为何值时,PM与⊙O相切?
(3)写出△PQR的面积S随动点移动时间t的函数关系式,并求S的最小值及相应的t值;
(4)是否存在△APQ为等腰三角形?若存在,求出相应的t值;若不存在请说明理由.
【答案】
(1)30°
(2)解:如图1,连接OP,OM. 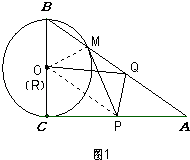
当PM与⊙O相切时,有∠PMO=∠PCO=90°,
∵MO=CO,PO=PO,
∴Rt△PMO≌Rt△PCO,
∴∠MOP=∠COP;
由(1)知∠OBA=60°,
∵OM=OB,
∴△OBM是等边三角形,
∴∠BOM=60°,
∴∠MOP=∠COP=60°,
∴CP=COtan∠COP=6tan60°=6 ![]() ,
,
又∵ ![]()
∴2 ![]() t=6
t=6 ![]()
∴t=3,
即:t=3s时,PM与⊙O相切;
(3)解:如图2,过点Q作QE⊥AC于点E,
∵∠BAC=30°,AQ=4t,
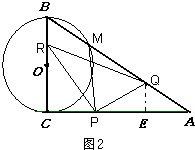
∴ ![]() AE=AQcos∠BAC=4tcos30°=2
AE=AQcos∠BAC=4tcos30°=2 ![]() t,
t,
∴ ![]()
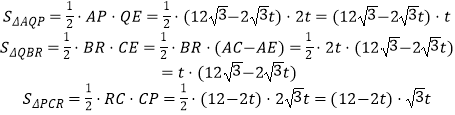
∴S△PQR=S△ACB﹣S△AQP﹣S△QBR﹣S△PCR
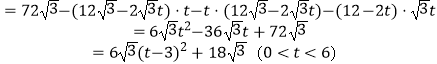 ,
,
∴当t=3s时, ![]() cm2;
cm2;
(4)解:存在.如图3,
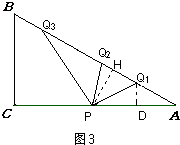
分三种情况:
①PQ1=AQ1=4t时,过点Q1作Q1D⊥AC于点D,
则 ![]() ,
,
∴ ![]() ,
,
∴t=2;
②当AP=AQ2=4t时,
∵ ![]() ,
,
∴ ![]()
![]() ,
,
③当PA=PQ3=4t时,
过点P作PH⊥AB于点H,
AH=PAcos30°= ![]() =18﹣3tAQ3=2AH=36﹣6t,
=18﹣3tAQ3=2AH=36﹣6t,
∴36﹣6t=4t,
∴t=3.6,
综上所述,当 ![]() s时,△APQ是等腰三角形.
s时,△APQ是等腰三角形.
【解析】解:(1)∵∠C=90°,CA=12 ![]() cm,BC=12cm,
cm,BC=12cm,
∴tan∠CAB= ![]() ,
,
∴∠CAB=30°,
所以答案是:30°;
【考点精析】根据题目的已知条件,利用锐角三角函数的定义和特殊角的三角函数值的相关知识可以得到问题的答案,需要掌握锐角A的正弦、余弦、正切、余切都叫做∠A的锐角三角函数;分母口诀:30度、45度、60度的正弦值、余弦值的分母都是2,30度、45度、60度的正切值、余切值的分母都是3,分子口诀:“123,321,三九二十七”.


科目:初中数学 来源: 题型:
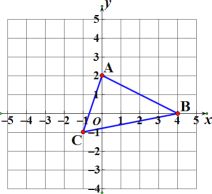
【题目】如图,在边长为 1 的正方形网格中,三角形 ABC 中任意一点 P(x0,y0)经平移后对应点为 P1(x0-4,y0+3),已知 A(0,2),B(4,0),C(-1,-1),将三角形 ABC 作同样的平移得到三角形 A1B1C1
(1)直接写出坐标:A1( , ),B1( , ),C1( , );
(2)三角形 A1B1C1 的面积为 ;
(3)已知点 P 在 y 轴上,且三角形 PAC 的面积等于三角形 ABC 面积的一半,求 P 点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查中,适宜采用全面调查(普查)方式的是( )
A. 对我市市民实施低碳生活情况的调查
B. 对我国首架大型民用飞机零部件的检查
C. 对全国中学生心理健康现状的调查
D. 对市场上的冰淇淋质量的调查
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,海中有一灯塔P,它的周围8海里内有暗礁.海轮以18海里/时的速度由西向东航行,在A处测得灯塔P在北偏东60°方向上;航行40分钟到达B处,测得灯塔P在北偏东30°方向上;如果海轮不改变航线继续向东航行,有没有触礁的危险?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】你能找出规律吗?
(1)计算:![]() = ,
= , ![]() = ,
= ,![]() = ,
= ,![]() = .
= .
(2)请按找到的规律计算:![]() ;
;
(3)已知:a=![]() ,b=
,b=![]() ,则
,则![]() = (用含a、b的式子表示).
= (用含a、b的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,以AB上一点O为圆心,OA长为半径的圆与BC相切于点D,分别交AC、AB于点E、F.若AC=6,AB=10,则⊙O的半径为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中:①过一点有且只有一条直线与已知直线平行;②过一点有且只有一条直线与已知直线垂直;③垂直于同一直线的两条直线互相平行;④平行于同一直线的两条直线互相平行;⑤两条直线被第三条直线所截,如果同旁内角相等,那么这两条直线互相平行;⑥连结![]() 、
、![]() 两点的线段就是
两点的线段就是![]() 、
、![]() 两点之间的距离,其中正确的有( )
两点之间的距离,其中正确的有( )
A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com