
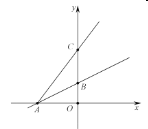
【题目】如图,在平面直角坐标系![]() 中,直线
中,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 、
、![]() ,点
,点![]() 是
是![]() 轴正半轴上的一点,当
轴正半轴上的一点,当![]() 时,则点
时,则点![]() 的纵坐标是( )
的纵坐标是( )
A.2B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
首先过点B作BD⊥AC于点D,设BC=a,根据直线解析式得到点A、B坐标,从而求出OA 、OB的长,易证△BCD ≌△ACO,再根据相似三角形的对应边成比例得出比例式,即可解答.
解:过点B作BD⊥AC于点D,设BC=a,

∵直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 、
、![]() ,
,
∴A(-2,0),B(0,1),即OA=2, OB=1,AC=![]() ,
,
∵![]() ,
,
∴AB平分∠CAB,
又∵BO⊥AO,BD⊥AC,
∴BO= BD=1,
∵∠BCD =∠ACO,∠CDB=∠COA =90°,
∴△BCD ≌△ACO,
∴![]() ,即a:
,即a:![]() =1:2
=1:2
解得:a1=![]() , a2=-1(舍去),
, a2=-1(舍去),
∴OC=OB+BC=![]() +1=
+1=![]() ,所以点C的纵坐标是
,所以点C的纵坐标是![]() .
.
故选:D.


科目:初中数学 来源: 题型:
【题目】已知反比例函数y=![]() 的图象与一次函数y=kx+m的图象相交于点A(2,1).
的图象与一次函数y=kx+m的图象相交于点A(2,1).
(1)分别求出这两个函数的解析式;
(2)当x取什么范围时,反比例函数值大于0;
(3)若一次函数与反比例函数另一交点为B,且纵坐标为﹣4,当x取什么范围时,反比例函数值大于一次函数的值;
(4)试判断点P(﹣1,5)关于x轴的对称点P′是否在一次函数y=kx+m的图象上.
查看答案和解析>>
科目:初中数学 来源: 题型:
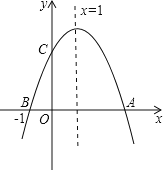
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于C点,且对称轴为x=1,点B坐标为(﹣1,0),则下面的四个结论,其中正确的个数为( )
①2a+b=0②4a﹣2b+c<0③ac>0④当y>0时,﹣1<x<4
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
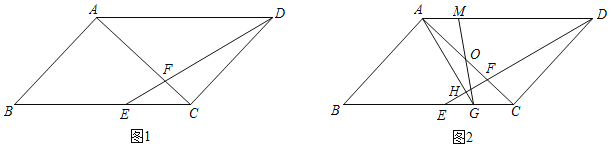
【题目】如图,在平行四边形ABCD中,连接AC,∠BAC=90°,AB=AC,点E是边BC上一点,连接DE,交AC于点F,∠ADE=30°.
(1)如图1,若AF=2,求BC的长;
(2)如图2,过点A作AG⊥DE于点H,交BC于点G,点O是AC中点,连接GO并延长交AD于点M.求证:AG+CG=DM.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两名同学做摸球游戏,他们把三个分别标有1,2,3的大小和形状完全相同的小球放在一个不透明的口袋中.
(1)求从袋中随机摸出一球,标号是1的概率;
(2)从袋中随机摸出一球后放回,摇匀后再随机摸出一球,若两次摸出的球的标号之和为偶数时,则甲胜;若两次摸出的球的标号之和为奇数时,则乙胜;试分析这个游戏是否公平?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小颖家经营着一家水果店,在杨梅旺销季节,她的父母经常去果园采购杨梅用于销售.果园的杨梅价格如下:购买数量不超过20筐,每筐进价20元;购买数量超过20筐,每筐进价18元.小颖在观察水果店一段时间的销售情况后发现,当杨梅的售价为每筐30元时,每天可销售30筐;每筐售价提高1元,每天销量减少1筐;每筐售价降低1元,每天销量增加1筐.若每天购进的杨梅能全部售出,且售价不低于进价,从果园进货的运费为每天100元.
(1)设售价为每筐![]() 元,则每天可售出___________筐.
元,则每天可售出___________筐.
(2)当每筐杨梅的售价定为多少元时,杨梅的日销售利润最大?最大日利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
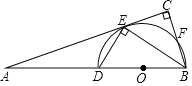
【题目】已知:如图,BD是半圆O的直径,A是BD延长线上的一点,BC⊥AE,交AE的延长线于点C,交半圆O于点F,且E为弧DF的中点.
(1)求证:AC是半圆O的切线;
(2)若BC=8,BE=6![]() ,求半径的长.
,求半径的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com