
【题目】如图,矩形ABCD中,AD=5,AB=6,点E为DC上一个动点,把△ADE沿AE折叠,点F为CD上一个动点,把△BCF沿BF折叠,当点D的对应点和点C的对应点都落在点D′处时,EF的长为 . 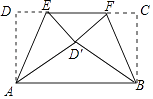
【答案】![]()
【解析】解:根据题意得△ADE≌△AD′E,△BCF≌△BD′F, ∴AD=AD′,BD′=BC,∠DAE=∠D′AE,∠CBF=∠D′BF,
∵矩形ABCD中,AD=BC,∠DAB=∠CBA=90°,
∴AD′=BD′,
∴∠D′AB=∠D′BA,
∴∠EAD′=∠FBD′,
∴△AED′≌△BFD′,
∴ED′=FD′,
∴DE=CF,
设DE=CF=D′E=D′F=x,
∴EF=6﹣2x,
过D′作D′G⊥AB于G反向延长交EF于H,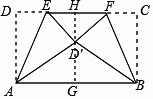
∵CD∥AB,
∴GH⊥EF,
则EH=HF=3﹣x,HG=AD=5,
∴D′G= ![]() =4,
=4,
∴HD′=1,
∵EH2+HD′2=ED′2 ,
∴(3﹣x)2+1=x2 ,
∴x= ![]() ,
,
∴EF= ![]() .
.
【考点精析】解答此题的关键在于理解矩形的性质的相关知识,掌握矩形的四个角都是直角,矩形的对角线相等,以及对翻折变换(折叠问题)的理解,了解折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图所示,△ABC≌△ADE,BC的延长线交AD于点F,交DE于点G,若∠CAD=20°,∠B=∠D=35°,∠EAB=120°,求∠AED,∠BFD以及∠DGB的度数.
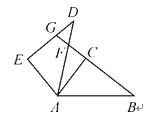
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九年级(1)班开展了为期一周的“敬老爱亲”社会活动,并根据学生做家务的时间来评价他们在活动中的表现.老师调查了全班50名学生在这次活动中做家务的时间,并将统计的时间(单位:小时)分成5组:A:0.5≤x<1,B:1≤x<1.5,C:1.5≤x<2,D:2≤x<2.5,E:2.5≤x<3,制作成两幅不完整的统计图(如图).
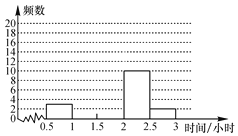
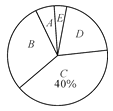
请根据图中提供的信息,解答下列问题:
(1)这次活动中学生做家务时间的中位数所在的组是____________;
(2)补全频数分布直方图;
(3)该班的小明同学这一周做家务2小时,他认为自己做家务的时间比班里一半以上的同学多,你认为小明的判断符合实际吗?请用适当的统计知识说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1,l2,l3上,且l1,l2之间的距离为2,l2,l3之间的距离为3,则AC的长是( )
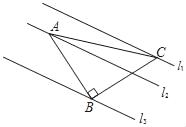
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解,回答下列问题:
![]()
![]()
![]()
(1)试猜想:1+3+5+7+9+…+2015+2017+2019的和是多少?
(2)推广:1+3+5+7+9+…+(2n-1)+(2n+1)的和是多少?
(3)计算:103+105+107+…+2017+2019.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,明亮同学在点A处测得大树顶端C的仰角为36°,斜坡AB的坡角为30°,沿在同一剖面的斜坡AB行走16米至坡顶B处,然后再沿水平方向行走6.4米至大树脚底点D处,那么大树CD的高度约为多少米?)(参考数据:sin36°≈0.59,cos36°≈0.81,tan36°≈0.73, ![]() ≈1.7).
≈1.7).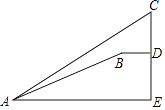
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在梯形ABCD中,AD∥BC,∠B=90°,BC=6,AD=3,∠DCB=30°.点E、F同时从B点出发,沿射线BC向右匀速移动,已知F点移动速度是E点移动速度的2倍,以EF为一边在CB的上方作等边△EFG,设E点移动距离为x(x>0).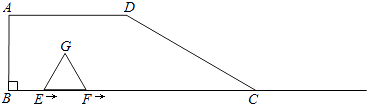
(1)△EFG的边长是(用含有x的代数式表示),当x=2时,点G的位置在;
(2)若△EFG与梯形ABCD重叠部分面积是y,求y与x之间的函数关系式;
(3)探究(2)中得到的函数y在x取何值时,存在最大值?并求出最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com