
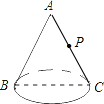
 如图,有一个圆锥,它的底面半径是2cm,母线长是8cm,在点B处有一只蚂蚁,它想吃到与B点相对且离圆锥顶点3$\sqrt{2}$cm 的点P处的食物,蚂蚁爬行的最短路程是2$\sqrt{5}$cm.
如图,有一个圆锥,它的底面半径是2cm,母线长是8cm,在点B处有一只蚂蚁,它想吃到与B点相对且离圆锥顶点3$\sqrt{2}$cm 的点P处的食物,蚂蚁爬行的最短路程是2$\sqrt{5}$cm. 分析 将圆锥侧面展开,进而根据平面上两点之间的距离,线段最短,求出最短路程.
解答 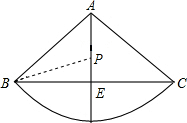 解:如图所示,
解:如图所示,
∵它的底面半径是2cm,母线长是8cm,
∴l=$\frac{nπ×{8}^{\;}}{180}$=4π,解得n=90°,
∵AB=AC,
∴∠ABC=∠ACB=45°.
∵AE⊥BC,
∴∠BAE=∠ABE=45°,
∴BE=AE,
设BE=AE=x,则2BE2=AB2,即2x2=82,解得x=4$\sqrt{2}$cm,
∵AP=3$\sqrt{2}$cm,
∴PE=$\sqrt{2}$cm,
∴BP=$\sqrt{{BE}^{2}+{PE}^{2}}$=$\sqrt{{(3\sqrt{2})}^{2}+{(\sqrt{2})}^{2}}$=2$\sqrt{5}$(cm).
故答案为:2$\sqrt{5}$cm.
点评 本考查的是平面展开-最短路径问题,根据题意画出圆锥的侧面展开图,利用勾股定理求解是解答此题的关键.


科目:初中数学 来源: 题型:填空题
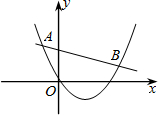 已知二次函数y1=ax2+bx+c与一次函数y2=kx+m(k≠0)的图象相交于点A(-2,4),B(8,2).如图所示,则能使y1>y2成立的x的取值范围是x<-2或x>8.
已知二次函数y1=ax2+bx+c与一次函数y2=kx+m(k≠0)的图象相交于点A(-2,4),B(8,2).如图所示,则能使y1>y2成立的x的取值范围是x<-2或x>8.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{{\sqrt{2}-1}}=\sqrt{2}-1$ | B. | $\frac{1}{{\sqrt{50}}}=\frac{{\sqrt{2}}}{5}$ | C. | $\sqrt{1000}=10\sqrt{5}$ | D. | $\sqrt{9-2\sqrt{14}}=\sqrt{7}-\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
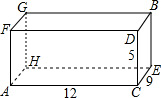 有一长方体纸盒,如图所示,小明所在的数学兴趣小组研究由长方体的底面A点到长方体中与A点相对的B点最短距离.若长方体的底面边长为12,宽为9,高为5,请你帮助该小组计算出由A到B的最短路线.(21.592≈466,18.442≈340,结果保留两位小数)
有一长方体纸盒,如图所示,小明所在的数学兴趣小组研究由长方体的底面A点到长方体中与A点相对的B点最短距离.若长方体的底面边长为12,宽为9,高为5,请你帮助该小组计算出由A到B的最短路线.(21.592≈466,18.442≈340,结果保留两位小数)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3a+8的意义是3a与8的和 | |
| B. | 4(m+3)的意义是4与m+3的积 | |
| C. | a2-2b的意义是a的平方与b的差的2倍 | |
| D. | a2+b2的意义是a与b的平方和 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
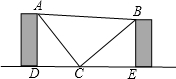 一个等腰直角三角板如图搁置在两柜之间,且点D,C,E在同一直线上,已知稍高的柜高AD为80cm,两柜距离DE为140cm.求稍矮的柜高BE.
一个等腰直角三角板如图搁置在两柜之间,且点D,C,E在同一直线上,已知稍高的柜高AD为80cm,两柜距离DE为140cm.求稍矮的柜高BE.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
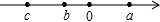 若有理数a,b,c在数轴上的位置如图所示,请化简:|ab3|=-ab3;|a+c|=-a-c;|b-c|=b-c;|b-c|-|b-a|=2b-c-a.
若有理数a,b,c在数轴上的位置如图所示,请化简:|ab3|=-ab3;|a+c|=-a-c;|b-c|=b-c;|b-c|-|b-a|=2b-c-a.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com