
【题目】如图,△ABC是等边三角形,延长BC到E,使CE=![]() BC.点D是边AC的中点,连接ED并延长ED交AB于F,求证:
BC.点D是边AC的中点,连接ED并延长ED交AB于F,求证:
(1)EF⊥AB;(2)DE=2DF.
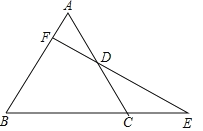
【答案】(1)见解析;(2)见解析
【解析】
(1)根据等边三角形的性质得出AC=BC,∠ACB=∠B=60°,求出CD=CE,根据三角形外角性质和等腰三角形的性质求出∠E=30°,求出∠BFE即可;
(2)连接BD,求出BD=DE,根据含30°角的直角三角形的性质得出BD=2DF,即可得出答案.
证明:(1)∵△ABC是等边三角形,
∴AC=BC,∠ACB=∠B=60°,
∵D为AC的中点,
∴AD=CD=![]() AC,
AC,
∵CE=![]() BC,
BC,
∴CD=CE,
∵∠E+∠CDE=∠ACB=60°,
∴∠E=∠CDE=30°,
∵∠B=60°,
∴∠EFB=180°﹣60°﹣30°=90°,
即EF⊥AB;
(2)连接BD,

∵△ABC是等边三角形,
∴AB=BC,∠ABC=60°,
∵D为AC的中点,
∴∠DBC=∠ABD=![]() ∠ABC=30°,
∠ABC=30°,
∵∠E=30°,
∴∠DBC=∠E,
∴DE=BD,
∵∠BFE=90°,∠ABD=30°,
∴BD=2DF,
即DE=2DF.


科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,C是⊙O上一点,过点C的直线交AB的延长线于点D,AE⊥DC,垂足为E,F是AE与⊙O的交点,AC平分∠BAE.

(1)求证:DE是⊙O的切线;
(2)若AE=6,∠D=30°,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场将进货价为30元的台灯以40元的价格售出,平均每月能售出600个,这种台灯的售价每上涨1元,其销量就减少10个,
(1)为了实现销售这种台灯平均每月10000元的销售利润,售价应定为多少元?
(2)当售价定为多少元时,其销售利润达到最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,抛物线![]() ( a≠0)经过原点,顶点为A(h,k)(h≠0).
( a≠0)经过原点,顶点为A(h,k)(h≠0).
(1)当h=1,k=2时,求抛物线的解析式;
(2)若抛物线![]() (t≠0)也经过A点,求a与t之间的关系式;
(t≠0)也经过A点,求a与t之间的关系式;
(3)当点A在抛物线![]() 上,且-2≤h<1时,求a的取值范围.
上,且-2≤h<1时,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
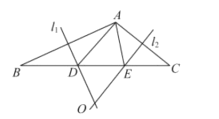
【题目】如图,在△ABC中,边AB的垂直平分线OM与边AC的垂直平分线ON交于点O,分别交BC于点D、E,已知△ADE的周长5cm.
(1)求BC的长;
(2)分别连接OA、OB、OC,若△OBC的周长为13cm,求OA的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是中国古代张苍、耿寿昌所撰写的一部数学专著 .是《算经十书》中最重要的一部,成于公元一世纪左右 .全书总结了战国、秦、汉时期的数学成就 .同时,《九章算术》在数学上还有其独到的成就,不仅最早提到分数问题,也首先记录了盈不足等问题,其中有一个数学问题“今有垣厚一丈,两鼠对穿 .大鼠日一尺,小鼠亦一尺 .大鼠日自倍,小鼠日自半 .问:何日相逢?”.译文:“有一堵一丈(旧制长度单位,1丈=10尺=100寸)厚的墙,两只老鼠从两边向中间打洞 .大老鼠第一天打一尺,小老鼠也是一尺 .大老鼠每天的打洞进度是前一天的一倍,小老鼠每天的进度是前一天的一半 .问它们几天可以相逢?”请你用所学数学知识方法给出答案:______________ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请按照研究问题的步骤依次完成任务.
(问题背景)
(1)如图1的图形我们把它称为“8字形”, 请说理证明∠A+∠B=∠C+∠D.
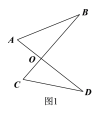
(简单应用)
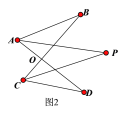
(2)如图2,AP、CP分别平分∠BAD、∠BCD,若∠ABC=20°,∠ADC=26°,求∠P的度数(可直接使用问题(1)中的结论)
(问题探究)
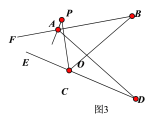
(3)如图3,直线AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE, 若∠ABC=36°,∠ADC=16°,猜想∠P的度数为 ;
(拓展延伸)
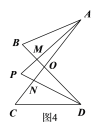
(4)在图4中,若设∠C=x,∠B=y,∠CAP=![]() ∠CAB,∠CDP=
∠CAB,∠CDP=![]() ∠CDB,试问∠P与∠C、∠B之间的数量关系为 (用x、y表示∠P) ;
∠CDB,试问∠P与∠C、∠B之间的数量关系为 (用x、y表示∠P) ;
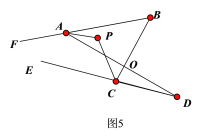
(5)在图5中,AP平分∠BAD,CP平分∠BCD的外角∠BCE,猜想∠P与∠B、D的关系,直接写出结论 .
查看答案和解析>>
科目:初中数学 来源: 题型:
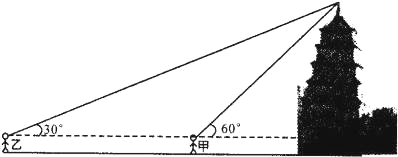
【题目】又到了一年中的春游季节,某班学生利用周末到白塔山去参观“晏阳初博物馆”.下面是两位同学的一段对话:
甲:我站在此处看塔顶仰角为60°;
乙:我站在此处看塔顶仰角为30°;
甲:我们的身高都是1.5m;
乙:我们相距20m.
请你根据两位同学的对话,计算白塔的高度.(精确到1米)
查看答案和解析>>
科目:初中数学 来源: 题型:
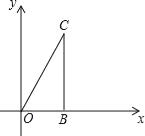
【题目】已知,如图,△OBC中是直角三角形,OB与x轴正半轴重合,∠OBC=90°,且OB=1,BC=![]() ,将△OBC绕原点O逆时针旋转60°再将其各边扩大为原来的2倍,使OB1=OC,得到△OB1C1,将△OB1C1绕原点O逆时针旋转60°再将其各边扩大为原来的2倍,使OB2=OC1,得到△OB2C2,…,如此继续下去,得到△OB2015C2015,则点C2015的坐标是_____.
,将△OBC绕原点O逆时针旋转60°再将其各边扩大为原来的2倍,使OB1=OC,得到△OB1C1,将△OB1C1绕原点O逆时针旋转60°再将其各边扩大为原来的2倍,使OB2=OC1,得到△OB2C2,…,如此继续下去,得到△OB2015C2015,则点C2015的坐标是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com