
【题目】某商场将进货价为30元的台灯以40元的价格售出,平均每月能售出600个,这种台灯的售价每上涨1元,其销量就减少10个,
(1)为了实现销售这种台灯平均每月10000元的销售利润,售价应定为多少元?
(2)当售价定为多少元时,其销售利润达到最大,最大利润是多少?
【答案】(1)50或80; (2) 售价为65元时利润最大,利润最大为12250元;
【解析】
(1) 假设这种台灯上涨x元,根据题意列出方程![]() ,再求解即可得到答案;
,再求解即可得到答案;
(2)根据利润=每个台灯的利润×销售量列出一元二次方程,再根据二次函数的性质求最大利润即可得到答案;
解:(1) 假设这种台灯上涨x元,根据题意可得方程:
![]() ,
,
即:![]() ,
,
化简得:![]() ,
,
即:![]()
解得:![]() 或
或![]() ,
,
此时售价定价为:10+40=50(元)或者40+40=80(元);
(2)设台灯售价为x元,利润为y元,根据题意得:
![]() ,
,
即:![]() ,
,
化简得:![]()
即:![]() ,
,
根据二次函数的性质,开口向下,越靠近对称轴的点对应的值越大,对称轴处取得最大值,
因此,当x=65时,取得最大利润y=12250;
故售价为65元时利润最大为12250元;


科目:初中数学 来源: 题型:
【题目】如图,AD是等边三角形ABC的高,点E是AD上的一个动点(点E不与点A重合),连接CE,将线段CE绕点E顺时针旋转60°得到EF,连接BF、CF.
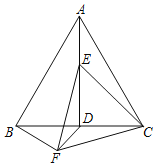
(1)猜想:△CEF是 三角形;
(2)求证:AE=BF;
(3)若AB=4,连接DF,在点E运动的过程中,请直接写出DF的最小值 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(a﹣2b,2﹣4ab)在抛物线y=x2+4x+10上,则点A关于抛物线对称轴的对称点坐标为( )
A. (﹣3,7) B. (﹣1,7) C. (﹣4,10) D. (0,10)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设函数![]() (
(![]() 为常数),下列说法正确的是( ).
为常数),下列说法正确的是( ).
A. 对任意实数![]() ,函数与
,函数与![]() 轴都没有交点
轴都没有交点
B. 存在实数![]() ,满足当
,满足当![]() 时,函数
时,函数![]() 的值都随
的值都随![]() 的增大而减小
的增大而减小
C. ![]() 取不同的值时,二次函数
取不同的值时,二次函数![]() 的顶点始终在同一条直线上
的顶点始终在同一条直线上
D. 对任意实数![]() ,抛物线
,抛物线![]() 都必定经过唯一定点
都必定经过唯一定点
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一座桥如图,桥下水面宽度AB是20米,高CD是4米.要使高为3米的船通过,则其宽度须不超过多少米.
(1)如图1,若把桥看做是抛物线的一部分,建立如图坐标系.
①求抛物线的解析式;
②要使高为3米的船通过,则其宽度须不超过多少米?
(2)如图2,若把桥看做是圆的一部分.
①求圆的半径;
②要使高为3米的船通过,则其宽度须不超过多少米?

查看答案和解析>>
科目:初中数学 来源: 题型:
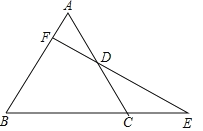
【题目】如图,△ABC是等边三角形,延长BC到E,使CE=![]() BC.点D是边AC的中点,连接ED并延长ED交AB于F,求证:
BC.点D是边AC的中点,连接ED并延长ED交AB于F,求证:
(1)EF⊥AB;(2)DE=2DF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个服装厂加工同种型号的防护服,甲厂每天加工的数量是乙厂每天加工数量的1.5倍,两厂各加工600套防护服,甲厂比乙厂要少用4天.
(1)求甲、乙两厂每天各加工多少套防护服?
(2)已知甲、乙两厂加工这种防护服每天的费用分别是150元和120元,疫情期间,某医院紧急需要3000套这种防护服,甲厂单独加工一段时间后另有安排,剩下任务只能由乙单独完成.如果总加工费不超过6360元,那么甲厂至少要加工多少天?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com