
����Ŀ����ͼ1����֪������C1��![]() ��x��������ύ�ڵ�A����BΪ�����ߵĶ��㣬ֱ��l��
��x��������ύ�ڵ�A����BΪ�����ߵĶ��㣬ֱ��l��![]() ��һ����ֱ�ߣ�
��һ����ֱ�ߣ�
(1)���A����B�����ꣻ
(2)��ֱ��l������Aʱ�����ֱ��l�Ľ���ʽ����ֱ��д����ʱ��![]() ʱ���Ա���x��ȡֵ��Χ��
ʱ���Ա���x��ȡֵ��Χ��
(3)��ͼ2����������C1��x���Ϸ��IJ�����x�ᷭ�ۣ���C1��x���·���ͼ����ϳ�һ���µ�ͼ��C2����ֱ��l�����ͼ��C2����ֻ����������ʱ��ֱ��д��k��ȡֵ��Χ��
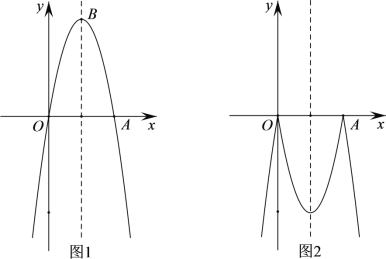
���𰸡�(1)A(2, 0)��B(1��3)��(2)x>2��x<![]() ��(3)
��(3)![]() ��k<0
��k<0
��������
��1����ʽ�������A��B�����ꣻ
��2��A�����ֱ�ߣ�����������ʽ������y1��y2�������ֱ�߽���ʽ�����ͼ����÷���Ҫ���x��ȡֵ��Χ��
��3�����ͼ��۲죬![]() ��k<0ʱ��ֻ����������.
��k<0ʱ��ֻ����������.
(1)��y=0��![]() ��
��
��ã�![]()
![]() ��
��
��A(2, 0)��
��![]() ��
��
��x=1ʱ��y=3��
��B(1��3)
(2)��A(2��0)����![]() ��
�У�![]()
��ֱ�߽���ʽΪ��![]() ��
��
����������������ͼ����һ����Ϊ��-![]() ��-
��-![]() ����
����
���ͼ��![]() ʱ��
ʱ��
x>2��x<![]() ��
��
(3)��ͼ���֪����ֱ�߾���A��ʱ��ǡ���������㣬
��ֱ�������˶�ʱ��ֻ���������㣬
��![]() ʱ��ǡ���������㣻
ʱ��ǡ���������㣻
��k<0ʱ���������������㣬����������
��![]() ��k<0.
��k<0.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
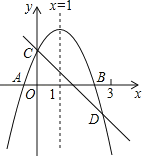
����Ŀ����ͼ��ʾ����֪���κ���y=ax2+bx+c��ͼ����x�ύ��A��B���㣬��y�ύ�ڵ�C�Գ���Ϊֱ��x=1��ֱ��y=��x+c��������y=ax2+bx+c����C��D���㣬D����x���·��Һ�����С��3�������н��ۣ�
��2a+b+c��0����a��b+c��0����x��ax+b����a+b����a����1��
������ȷ���У�������
A. 4�� B. 3�� C. 2�� D. 1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�����ͷ������ʣ��ס��������˹�˾���ɳ�һ���������ֱ�Ӿ�Ŀ�ĵ�240ǧ��270ǧ������ͬʱ��������Ԯ��������֪�ҹ�˾������ƽ���ٶ��Ǽ�˾������ƽ���ٶȵ�1.5������˾�Ŀ������ҹ�˾�Ŀ�����1Сʱ����Ŀ�ĵأ��ֱ���ס��������˹�˾������ƽ���ٶȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ����ѧ��������������ѧУ�ƻ�������������ѡ�Σ�A���鷨��B���滭��C��������D���赸��Ϊ�˽�ѧ�������Ź��ε�ϲ���������ȫУ��Χ�������ȡ������ѧ�������ʾ����飨ÿ���������ѧ������ѡ�����ֻ��ѡ������һ�ţ��������ݽ��������������Ƴ�����������������ͳ��ͼ������ͼ��������Ϣ����������⣺
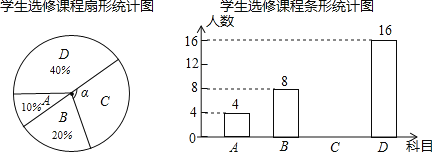
��1�����ε����ѧ�����ж����ˣ�����ͳ��ͼ�С����Ķ����Ƕ��٣�
��2���������ͳ��ͼ����������
��3��ѧУΪ�ٰ�2018���У�Ļ������ڣ�������A���鷨��B���滭��C��������D���赸����������ʽ��ѡ�������������һ���µĽ�Ŀ��ʽ�������б�������״ͼ���ѡ���鷨�����������һ��ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ա�ǰϦ��ijУ��չ�ˡ��������ҳɳ������Ķ����Ϊ���˽��Уѧ���ڴ˴λ�п����Ķ��鼮����������������ȡ�˲���ѧ�����е��飬���ռ��������ݽ������������Ƴ�������������ͳ��ͼ�������ͳ��ͼ��Ϣ����������⣺
��1���ε����й���ȡ��ѧ��������
��2����ȫ����ͳ��ͼ��
��3��������ͳ��ͼ�У��Ķ�![]() ���鼮�������������ε�Բ�ĽǶ������� ����
���鼮�������������ε�Բ�ĽǶ������� ����
��4������У��![]() ��ѧ�������Ƹ�У����λ���Ķ��鼮������������
��ѧ�������Ƹ�У����λ���Ķ��鼮������������![]() ����ѧ���ж����ˣ�
����ѧ���ж����ˣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
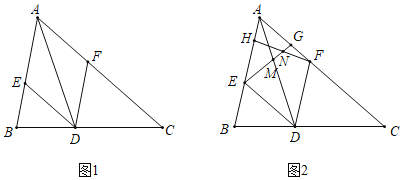
����Ŀ���ڡ�ABC�У���BAC=60����ADƽ�֡�BAC����BC�ڵ�D���ֱ��D��DE��AC����AB�ڵ�E��DF��AB����AC�ڵ�F��
(1)��ͼ1�����ж��ı���AEDF����״����˵�����ɣ�
(2)��ͼ2����AD=4![]() ����H��G�ֱ����߶�AE��AF�ϣ���EH=AG=3������EG��AD�ڵ�M������FH��EG�ڵ�N��
����H��G�ֱ����߶�AE��AF�ϣ���EH=AG=3������EG��AD�ڵ�M������FH��EG�ڵ�N��
(i)��ENEG��ֵ��
(ii)���߶�DM�Ƶ�D˳ʱ����ת60���õ��߶�DM������֤��H��F��M��������ͬһ��ֱ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ѧħ����ħ��ʦ���������һ������Ȼ������������²��������
![]()
ħ��ʦ������˵����������Ǹ�����
��1�����С���������![]() ������ͨ���������������ħ��ʦ�Ľ����
������ͨ���������������ħ��ʦ�Ľ����
��2�����С������һ�����������ħ��ʦ���Ϊ85����ôħ��ʦ����˵��С������Ǹ����ǣ�__________��
��3�������ֽ����˼��γ��ԣ�ħ��ʦ��������˵����������Ǹ�������������������Ϊ![]() �����㰴��ħ��ʦҪ�����������д���ʽ����������һ�仰˵�����ħ���İ��
�����㰴��ħ��ʦҪ�����������д���ʽ����������һ�仰˵�����ħ���İ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �DZ߳�Ϊ
�DZ߳�Ϊ![]() ��������
��������![]() �ĶԽ���
�ĶԽ���![]() �ϵĶ��㣬����
�ϵĶ��㣬����![]() �ֱ���
�ֱ���![]() �ڵ�
�ڵ�![]()
![]() �ڵ�
�ڵ�![]() ������
������![]() ���ӳ���������
���ӳ���������![]() �ڵ�
�ڵ�![]() ������
������![]() �ڵ�
�ڵ�![]() ������
������![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() ����
����![]() ���˶�ʱ(������
���˶�ʱ(������![]() ����)�����½��ۣ���
����)�����½��ۣ���![]() ����
����![]() ����
����![]() ����
����![]() ����Сֵ��
����Сֵ��![]() ��������ȷ����_______��(������Ϊ��ȷ���۵���Ŷ�����)
��������ȷ����_______��(������Ϊ��ȷ���۵���Ŷ�����)

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
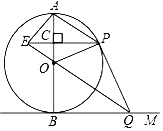
����Ŀ����ͼ��AB�ǡ�O��ֱ����BM�С�O�ڵ�B����P�ǡ�O�ϵ�һ�����㣨��P����A��B�����غϣ�������AP������O��OQ��AP��BM�ڵ�Q������P��PE��AB�ڵ�C����QO���ӳ����ڵ�E������PQ��OP��AE��
��1����֤��ֱ��PQΪ��O�����ߣ�
��2����ֱ��AB�ij�Ϊ4��
�ٵ�PE���� ��ʱ���ı���BOPQΪ�����Σ�
�ڵ�PE���� ��ʱ���ı���AEOPΪ���Σ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com