
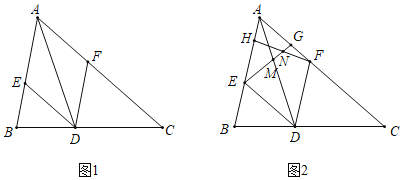
【题目】在△ABC中,∠BAC=60°,AD平分∠BAC交边BC于点D,分别过D作DE∥AC交边AB于点E,DF∥AB交边AC于点F.
(1)如图1,试判断四边形AEDF的形状,并说明理由;
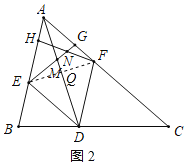
(2)如图2,若AD=4![]() ,点H,G分别在线段AE,AF上,且EH=AG=3,连接EG交AD于点M,连接FH交EG于点N.
,点H,G分别在线段AE,AF上,且EH=AG=3,连接EG交AD于点M,连接FH交EG于点N.
(i)求ENEG的值;
(ii)将线段DM绕点D顺时针旋转60°得到线段DM′,求证:H,F,M′三点在同一条直线上
【答案】(1) 四边形AEDF的形状是菱形,理由见解析;(1) (i) 12;(ii)见解析
【解析】
(1)由题意得出四边形AEDF是平行四边形;再根据角平分线性质及平行线性质可推出∠EAD=∠EDA;根据等角对等边得出AE=DE即可得出;
(2) (i) 连接EF交AD于点Q,根据菱形的性质得出△AEF是等边三角形,再根据余弦得出AE=AF=EF=4,根据SAS得出△AEG≌△EFH,根据全等三角形性质得出△AEG∽△NEH,最后根据相似三角形的性质得出答案;
(ii) 连接FM',根据等边三角形的性质及旋转的性质可得出△EDM≌△FDM',再根据全等三角形性质、等量代换即可得出答案.
(1)解:四边形AEDF的形状是菱形;理由如下:
∵DE∥AC,DF∥AB,
∴四边形AEDF是平行四边形,
∵AD平分∠BAC,
∴∠EAD=∠FAD,
∵DE∥AC,
∴∠EDA=∠FAD,
∴∠EAD=∠EDA,
∴AE=DE,
∴四边形AEDF是菱形;
(2)(i)解:连接EF交AD于点Q,如图2所示:
∵∠BAC=60°,四边形AEDF是菱形,
∴∠EAD=30°,AD、EF相互垂直平分,△AEF是等边三角形,
∴∠EAF=∠AEF=∠AFE=60°,
∵AD=![]() ,
,
∴AQ=![]() ,
,
在Rt△AQE中,cos∠EAQ=![]() ,即cos30°=
,即cos30°=![]() ,
,
∴AE=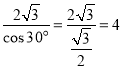 ,
,
∴AE=AF=EF=4,
在△AEG和△EFH中, ,
,
∴△AEG≌△EFH(SAS),
∴∠AEG=∠EFH,
∴∠ENH=∠EFH+∠GEF=∠AEG+∠GEF=60°,
∴∠ENH=∠EAG,
∵∠AEG=∠NEH,
∴△AEG∽△NEH,
∴![]() ,
,
∴ENEG=EHAE=3×4=12;
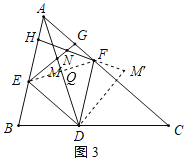
(ii)证明:如图3,连接FM',
∵DE∥AC,
∴∠AED=180°﹣∠BAC=120°,
由(1)得:△EDF是等边三角形,
∴DE=DF,∠EDF=∠FED=∠EFD=60°,
由旋转的性质得:∠MDM'=60°,DM=DM',
∴∠EDM=∠FDM',
在△EDM和△FDM'中,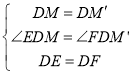 ,
,
∴△EDM≌△FDM'(SAS),
∴∠MED=∠DFM',
由(i)知,∠AEG=∠EFH,
∴∠DFM'+∠EFH=∠MED+∠AEG=∠AED=120°,
∴∠HFM'=∠DFM'+∠HFE+∠EFD=120°+60°=180°,
∴H,F,M′三点在同一条直线上.


科目:初中数学 来源: 题型:
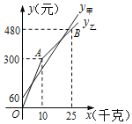
【题目】张庄甲、乙两家草莓采摘园的草莓销售价格相同,“春节期间”,两家采摘园将推出优惠方案,甲园的优惠方案是:游客进园需购买门票,采摘的草莓六折优惠;乙园的优惠方案是:游客进园不需购买门票,采摘园的草莓超过一定数量后,超过部分打折优惠.优惠期间,某游客的草莓采摘量为x(千克),在甲园所需总费用为y甲(元),在乙园所需总费用为y乙(元),y甲、y乙与x之间的函数关系如图所示,折线OAB表示y乙与x之间的函数关系.
(1)甲采摘园的门票是 元,乙采摘园优惠前的草莓单价是每千克 元;
(2)当x>10时,求y乙与x的函数表达式;
(3)游客在“春节期间”采摘多少千克草莓时,甲、乙两家采摘园的总费用相同.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB,CD为两个建筑物,建筑物AB的高度为60米,从建筑物AB的顶部A点测得建筑物CD的顶部C点的俯角∠EAC为30°,测得建筑物CD的底部D点的俯角∠EAD为45°,求建筑物CD的高度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,点E为对角线AC上一点,且AE![]() CB,连接DE并延长交BC于点G,过点A作AH⊥BE于点H,交BC于点F.以下结论:①BH
CB,连接DE并延长交BC于点G,过点A作AH⊥BE于点H,交BC于点F.以下结论:①BH![]() HE;②∠BEG
HE;②∠BEG![]() 45°;③△ABF ≌△DCG; ④4BH2
45°;③△ABF ≌△DCG; ④4BH2![]() BG·CD.其中正确结论的个数是( )
BG·CD.其中正确结论的个数是( )
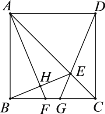
A.1个B.2
C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
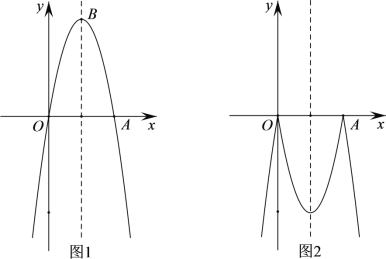
【题目】如图1,已知抛物线C1:![]() 与x轴的正半轴交于点A,点B为抛物线的顶点,直线l:
与x轴的正半轴交于点A,点B为抛物线的顶点,直线l:![]() 是一条动直线.
是一条动直线.
(1)求点A、点B的坐标;
(2)当直线l经过点A时,求出直线l的解析式,并直接写出此时当![]() 时,自变量x的取值范围;
时,自变量x的取值范围;
(3)如图2,将抛物线C1在x轴上方的部分沿x轴翻折,与C1在x轴下方的图形组合成一个新的图形C2,当直线l与组合图形C2有且只有两个交点时,直接写出k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,AB为⊙O的直径,D为![]() 的中点,过D作DF⊥AB于点E,交⊙O于点F,交弦BC于点G,连接CD,BF.
的中点,过D作DF⊥AB于点E,交⊙O于点F,交弦BC于点G,连接CD,BF.
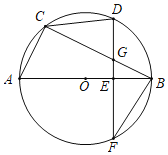
(1)求证:△BFG≌△DCG;
(2)若AC=10,BE=8,求BF的长;
(3)在(2)的条件下,P为⊙O上一点,连接BP,CP,弦CP交直径AB于点H,若△BPH与△CPB相似,求CP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在∠DAM内部做Rt△ABC,AB平分∠DAM,∠ACB=90°,AB=10,AC=8,点N为BC的中点,动点E由A点出发,沿AB运动,速度为每秒5个单位,动点F由A点出发,沿AM运动,速度为每秒8个单位,当点E到达点B时,两点同时停止运动,过A、E、F作⊙O.
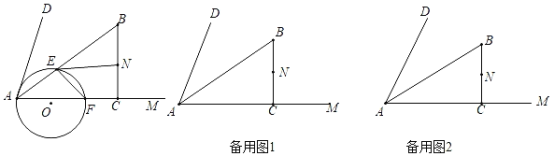
(1)判断△AEF的形状为 ,并判断AD与⊙O的位置关系为 ;
(2)求t为何值时,EN与⊙O相切,求出此时⊙O的半径,并比较半径与劣弧![]() 长度的大小;
长度的大小;
(3)直接写出△AEF的内心运动的路径长为 ;(注:当A、E、F重合时,内心就是A点)
(4)直接写出线段EN与⊙O有两个公共点时,t的取值范围为 .
(参考数据:sin37°=![]() ,tan37°=
,tan37°=![]() ,tan74°≈
,tan74°≈![]() ,sin74°≈
,sin74°≈![]() ,cos74°≈
,cos74°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 中
中![]() 点
点![]() 分别在边
分别在边![]() 、边
、边![]() 上,连接
上,连接![]() 点
点![]() 、点
、点![]() 在直线
在直线![]() 同侧,连接
同侧,连接![]() 且
且![]() .
.
(1)点![]() 与点
与点![]() 重合时,
重合时,
①如图1,![]() 时,
时,![]() 和
和![]() 的数量关系是 ;位置关系是 ;
的数量关系是 ;位置关系是 ;
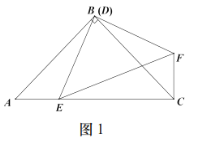
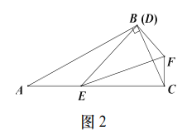
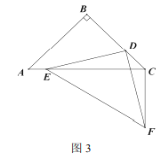
②如图2,![]() 时,猜想
时,猜想![]() 和
和![]() 的关系,并说明理由;
的关系,并说明理由;
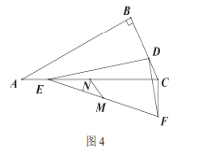
(2)![]() 时,
时,
③如图3,![]() 时,若
时,若![]() 求
求![]() 的长度;
的长度;
④如图4,![]() 时,点
时,点![]() 分别为
分别为![]() 和
和![]() 的中点,若
的中点,若![]() ,直接写出
,直接写出![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象与y轴正半轴相交,其顶点坐标为(![]() ,1),下列结论:①abc<0;②a+b=0;③4ac﹣b2=4a;④a+b+c<0.其中正确的有( )个.
,1),下列结论:①abc<0;②a+b=0;③4ac﹣b2=4a;④a+b+c<0.其中正确的有( )个.
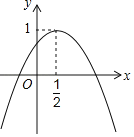
A.1B.2C.3D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com