
【题目】如图,二次函数y=ax2+bx+c的图象与y轴正半轴相交,其顶点坐标为(![]() ,1),下列结论:①abc<0;②a+b=0;③4ac﹣b2=4a;④a+b+c<0.其中正确的有( )个.
,1),下列结论:①abc<0;②a+b=0;③4ac﹣b2=4a;④a+b+c<0.其中正确的有( )个.
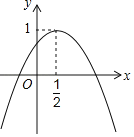
A.1B.2C.3D.4
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠BAC=60°,AD平分∠BAC交边BC于点D,分别过D作DE∥AC交边AB于点E,DF∥AB交边AC于点F.
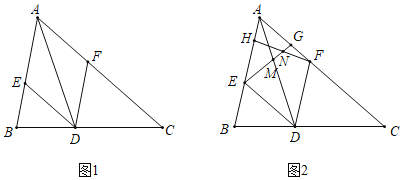
(1)如图1,试判断四边形AEDF的形状,并说明理由;
(2)如图2,若AD=4![]() ,点H,G分别在线段AE,AF上,且EH=AG=3,连接EG交AD于点M,连接FH交EG于点N.
,点H,G分别在线段AE,AF上,且EH=AG=3,连接EG交AD于点M,连接FH交EG于点N.
(i)求ENEG的值;
(ii)将线段DM绕点D顺时针旋转60°得到线段DM′,求证:H,F,M′三点在同一条直线上
查看答案和解析>>
科目:初中数学 来源: 题型:
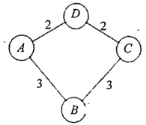
【题目】A,B,C,D四个地区爆发病毒疫情,它们之间的道路连通情况和距离(单位:km)如图所示,经调查发现,某地区受感染率与相邻地区自发病率和距离有关,具体公式为:
A地受B地的感染率![]() .已知A地受B地和D地感染率之相邻地区和为9%,D地的自发病率为24%.
.已知A地受B地和D地感染率之相邻地区和为9%,D地的自发病率为24%.
(1)求B地的自发病率;
(2)规定某地的危险系数等于该地的自发病率与总受感染率的和.
①若C地危险系数是A地危险系数的两倍,且D地受感染率比B地高5%,求A地的自发病率;
②在①的条件下,A地派出6支医疗队支援B,D两地,每派出1支医疗队,A地自身发病率上升0.75%,每支医疗队可以让被支援的地区的自发病率下降4%.在保证A地危险系数不上升的前提下,A地各派往B,D两地多少支队伍时,B地的自发病率下降最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
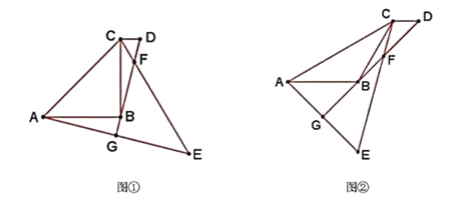
【题目】如图,在等腰△ABC中,AB=BC.CD∥AB,点D在点C的右侧,点A,E关于直线BD对称,CE交BD于点F,AE交DB延长线于点G.
(1)(猜想)
如图①,当∠ABC=90°时,∠EFG=________;
(2)(探究)
在(1)的前提下,若AB=4,CD=1,求EF的长;
(3)(应用)
如图②,当∠ABC=120°时,若EF=2 ![]() ,AB=2,则CD=________.
,AB=2,则CD=________.
查看答案和解析>>
科目:初中数学 来源: 题型:
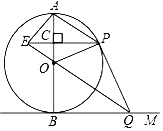
【题目】如图,AB是⊙O的直径,BM切⊙O于点B,点P是⊙O上的一个动点(点P不与A,B两点重合),连接AP,过点O作OQ∥AP交BM于点Q,过点P作PE⊥AB于点C,交QO的延长线于点E,连接PQ,OP,AE.
(1)求证:直线PQ为⊙O的切线;
(2)若直径AB的长为4.
①当PE= 时,四边形BOPQ为正方形;
②当PE= 时,四边形AEOP为菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
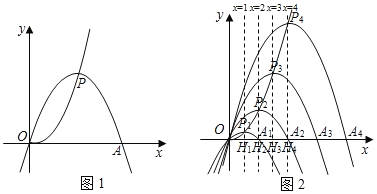
【题目】已知点P为抛物线y![]() x2上一动点,以P为顶点,且经过原点O的抛物线,记作“yp”,设其与x轴另一交点为A,点P的横坐标为m.
x2上一动点,以P为顶点,且经过原点O的抛物线,记作“yp”,设其与x轴另一交点为A,点P的横坐标为m.
(1)①当△OPA为直角三角形时,m= ;
②当△OPA为等边三角形时,求此时“yp”的解析式;
(2)若P点的横坐标分别为1,2,3,…n(n为正整数)时,抛物线“yp”分别记作“![]() ”、“
”、“![]() ”…,“
”…,“![]() ”,设其与x轴另外一交点分别为A1,A2,A3,…An,过P1,P2,P3,…Pn作x轴的垂线,垂足分别为H1,H2,H3,…Hn.
”,设其与x轴另外一交点分别为A1,A2,A3,…An,过P1,P2,P3,…Pn作x轴的垂线,垂足分别为H1,H2,H3,…Hn.
1)① Pn的坐标为 ;OAn= ;(用含n的代数式来表示)
②当PnHn﹣OAn=16时,求n的值.
2)是否存在这样的An,使得∠OP4An=90°,若存在,求n的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新冠肺炎疫情在全球蔓延,造成了严重的人员伤亡和经济损失,其中一个原因是新冠肺炎病毒传播速度非常快.一个人如果感染某种病毒,经过了两轮的传播后被感染的总人数将达到64人.
(1)求这种病毒每轮传播中一个人平均感染多少人?
(2)按照上面的传播速度,如果传播得不到控制,经过三轮传播后一共有多少人被感染?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com