
ΓΨΧβΡΩΓΩAΘ§BΘ§CΘ§DΥΡΗωΒΊ«χ±§ΖΔ≤ΓΕΨ“Ώ«ιΘ§ΥϋΟ«÷°ΦδΒΡΒά¬ΖΝ§Ά®«ιΩωΚΆΨύάκΘ®ΒΞΈΜΘΚkmΘ©»γΆΦΥυ ΨΘ§Ψ≠Βς≤ιΖΔœ÷Θ§Ρ≥ΒΊ«χ ήΗ–»Ψ¬ ”κœύΝΎΒΊ«χΉ‘ΖΔ≤Γ¬ ΚΆΨύάκ”–ΙΊΘ§ΨΏΧεΙΪ ΫΈΣΘΚ
AΒΊ ήBΒΊΒΡΗ–»Ψ¬ ![]() Θ°“―÷ΣAΒΊ ήBΒΊΚΆDΒΊΗ–»Ψ¬ ÷°œύΝΎΒΊ«χΚΆΈΣ9%Θ§DΒΊΒΡΉ‘ΖΔ≤Γ¬ ΈΣ24%Θ°
Θ°“―÷ΣAΒΊ ήBΒΊΚΆDΒΊΗ–»Ψ¬ ÷°œύΝΎΒΊ«χΚΆΈΣ9%Θ§DΒΊΒΡΉ‘ΖΔ≤Γ¬ ΈΣ24%Θ°
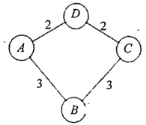
Θ®1Θ©«σBΒΊΒΡΉ‘ΖΔ≤Γ¬ ΘΜ
Θ®2Θ©ΙφΕ®Ρ≥ΒΊΒΡΈΘœ’œΒ ΐΒ»”ΎΗΟΒΊΒΡΉ‘ΖΔ≤Γ¬ ”κΉή ήΗ–»Ψ¬ ΒΡΚΆΘ°
ΔΌ»τCΒΊΈΘœ’œΒ ΐ «AΒΊΈΘœ’œΒ ΐΒΡΝΫ±ΕΘ§«“DΒΊ ήΗ–»Ψ¬ ±»BΒΊΗΏ5%Θ§«σAΒΊΒΡΉ‘ΖΔ≤Γ¬ ΘΜ
ΔΎ‘ΎΔΌΒΡΧθΦΰœ¬Θ§AΒΊ≈…≥ω6÷ß“ΫΝΤΕ”÷ß‘°BΘ§DΝΫΒΊΘ§ΟΩ≈…≥ω1÷ß“ΫΝΤΕ”Θ§AΒΊΉ‘…μΖΔ≤Γ¬ …œ…ΐ0Θ°75%Θ§ΟΩ÷ß“ΫΝΤΕ”Ω…“‘»Ο±Μ÷ß‘°ΒΡΒΊ«χΒΡΉ‘ΖΔ≤Γ¬ œ¬ΫΒ4%Θ°‘Ύ±Θ÷ΛAΒΊΈΘœ’œΒ ΐ≤Μ…œ…ΐΒΡ«ΑΧαœ¬Θ§AΒΊΗς≈…ΆυBΘ§DΝΫΒΊΕύ…Ό÷ßΕ”Έι ±Θ§BΒΊΒΡΉ‘ΖΔ≤Γ¬ œ¬ΫΒΉνΕύΘΩ
ΓΨ¥πΑΗΓΩΘ®1Θ©27%ΘΜΘ®2Θ©9%Θ®3Θ©AΒΊ≈…ΆυBΒΊ2÷ßΕ”ΈιΘ§≈…ΆυDΒΊ4÷ßΕ”ΈιΘΜ
ΓΨΫβΈωΓΩ
Θ®1Θ©…ηBΒΊΒΡΉ‘ΖΔΗ–»Ψ¬ ΈΣaΘ§”…Η–»Ψ¬ ΙΪ ΫΩ…«σΒΟAΒΊ ήBΒΊΚΆAΒΊ ήDΒΊΒΡΗ–»Ψ¬ Θ§“―÷ΣDΒΊΒΡΉ‘ΖΔ≤Γ¬ ΈΣ24%Θ§”…ΝΫΗ–»Ψ¬ ΚΆΈΣ9%Θ§Ω…«σΒΟBΒΊΒΡΉ‘ΖΔΗ–»Ψ¬ ΘΜΘ®2Θ©ΔΌ…ηAΒΊΒΡΉ‘ΖΔ≤Γ¬ ΈΣmΘ§CΒΊΒΡΉ‘ΖΔ≤Γ¬ ΈΣnΘ§“Ή«σΒΟAΒΊΚΆCΒΊΉή ήΗ–»Ψ¬ ΒΡΚΆΨυΈΣ9%Θ§Ω…ΒΟAΒΊΈΘœ’œΒ ΐΈΣ9%+mΘ§CΒΊΈΘœ’œΒ ΐΈΣ9%+mΘ§DΒΊ ήΗ–»Ψ¬ ΈΣ![]() Θ§B ήΗ–»Ψ¬ ΈΣ
Θ§B ήΗ–»Ψ¬ ΈΣ![]() Θ§”…“―÷ΣΧθΦΰΩ…Ν–≥ωΖΫ≥ΧΉιΘ§Φ¥Ω…«σΒΟmΘ§n÷ΒΘΜΔΎ…ηAΒΊ≈…ΆυBΒΊx÷ßΕ”ΈιΘ§≈…ΆυDΒΊy÷ßΕ”ΈιΘ§‘ρAΒΊΉ‘ΖΔΗ–»Ψ¬ ΈΣ9+0.75%ΓΝ6=13.5%Θ§AΒΊ ήBΒΊΗ–»Ψ¬ ΈΣ
Θ§”…“―÷ΣΧθΦΰΩ…Ν–≥ωΖΫ≥ΧΉιΘ§Φ¥Ω…«σΒΟmΘ§n÷ΒΘΜΔΎ…ηAΒΊ≈…ΆυBΒΊx÷ßΕ”ΈιΘ§≈…ΆυDΒΊy÷ßΕ”ΈιΘ§‘ρAΒΊΉ‘ΖΔΗ–»Ψ¬ ΈΣ9+0.75%ΓΝ6=13.5%Θ§AΒΊ ήBΒΊΗ–»Ψ¬ ΈΣ![]() Θ§AΒΊ ήDΒΊΗ–»Ψ¬ ΈΣ
Θ§AΒΊ ήDΒΊΗ–»Ψ¬ ΈΣ![]() Θ§x+y=6Θ§»τ±Θ÷ΛAΒΊΈΘœ’œΒ ΐ≤Μ…œ…ΐΘ§‘ρ13.5%+
Θ§x+y=6Θ§»τ±Θ÷ΛAΒΊΈΘœ’œΒ ΐ≤Μ…œ…ΐΘ§‘ρ13.5%+![]() Γή9%Θ§ΫΪx+y=6¥ζ»κΘ§ΫβΒΟxΓή2.7Θ§»ΓΉν¥σΒΡ’ϊ ΐ2Θ§Φ¥ΈΣ≈…»ΞBΒΊΒΡΕ”Έι ΐ.
Γή9%Θ§ΫΪx+y=6¥ζ»κΘ§ΫβΒΟxΓή2.7Θ§»ΓΉν¥σΒΡ’ϊ ΐ2Θ§Φ¥ΈΣ≈…»ΞBΒΊΒΡΕ”Έι ΐ.
Θ®1Θ©…ηBΒΊΒΡΉ‘ΖΔΗ–»Ψ¬ ΈΣaΘ§
”…Η–»Ψ¬ ΙΪ ΫΩ…Ν–≥ωΖΫ≥ΧΘ§
![]() +
+![]() =9%Θ§ΫβΒΟa=27%Θ§
=9%Θ§ΫβΒΟa=27%Θ§
ΓύBΒΊΒΡΉ‘ΖΔΗ–»Ψ¬ ΈΣ27%ΘΜ
Θ®2Θ©ΔΌ…ηAΒΊΒΡΉ‘ΖΔ≤Γ¬ ΈΣmΘ§CΒΊΒΡΉ‘ΖΔ≤Γ¬ ΈΣnΘ§
”…Η–»Ψ¬ ΙΪ ΫΩ…«σΒΟAΒΊΉή ήΗ–»ΨΒΡΚΆΈΣ![]() +
+![]() =9%Θ§
=9%Θ§
Ά§άμΘ§CΒΊΉή ήΗ–»Ψ¬ ΒΡΚΆΈΣ9%Θ§DΒΊ ήΗ–»Ψ¬ ΈΣ![]() Θ§B ήΗ–»Ψ¬ ΈΣ
Θ§B ήΗ–»Ψ¬ ΈΣ![]() Θ§
Θ§
ΓύAΒΊΈΘœ’œΒ ΐΈΣ9%+mΘ§CΒΊΈΘœ’œΒ ΐΈΣ9%+nΘ§
”…¥ΥΩ…Ν–≥ωΖΫ≥ΧΘ§
9%+n=2(9%+m)Θ§![]() Θ§
Θ§
ΫβΒΟm=9%Θ§n=27%ΘΜ
Φ¥AΒΊΒΡΉ‘ΖΔ≤Γ¬ ΈΣ9%ΘΜ
ΔΎ…ηAΒΊ≈…ΆυBΒΊx÷ßΕ”ΈιΘ§≈…ΆυDΒΊy÷ßΕ”ΈιΘ§
‘ρx+y=6Θ§
¥Υ ±AΒΊΉ‘ΖΔΗ–»Ψ¬ ΈΣ9+0.75%ΓΝ6=13.5%Θ§
AΒΊ ήBΒΊΗ–»Ψ¬ ΈΣ![]() Θ§AΒΊ ήDΒΊΗ–»Ψ¬ ΈΣ
Θ§AΒΊ ήDΒΊΗ–»Ψ¬ ΈΣ![]() Θ§
Θ§
”…Χβ“βΒΟ13.5%+![]() Γή9%Θ§ΫΪx+y=6¥ζ»κ≤ΜΒ» ΫΘ§
Γή9%Θ§ΫΪx+y=6¥ζ»κ≤ΜΒ» ΫΘ§
ΫβΒΟxΓή2.7Θ§»τ ΙBΒΊΒΡΉ‘ΖΔ≤Γ¬ œ¬ΫΒΉνΕύΘ§¥Υ ±x»ΓΉν¥σ÷Β2Θ§
Φ¥AΒΊ≈…ΆυBΒΊ2÷ßΕ”ΈιΘ§≈…ΆυDΒΊ4÷ßΕ”ΈιΘ§BΒΊΒΡΉ‘ΖΔ≤Γ¬ œ¬ΫΒΉνΕύ.



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§ABΘ§CDΈΣΝΫΗωΫ®÷ΰΈοΘ§Ϋ®÷ΰΈοABΒΡΗΏΕ»ΈΣ60ΟΉΘ§¥”Ϋ®÷ΰΈοABΒΡΕΞ≤ΩAΒψ≤βΒΟΫ®÷ΰΈοCDΒΡΕΞ≤ΩCΒψΒΡΗ©Ϋ«ΓœEACΈΣ30ΓψΘ§≤βΒΟΫ®÷ΰΈοCDΒΡΒΉ≤ΩDΒψΒΡΗ©Ϋ«ΓœEADΈΣ45ΓψΘ§«σΫ®÷ΰΈοCDΒΡΗΏΕ»Θ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
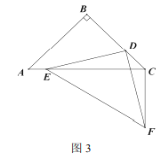
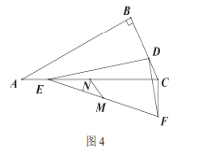
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΓœDAMΡΎ≤ΩΉωRtΓςABCΘ§ABΤΫΖ÷ΓœDAMΘ§ΓœACBΘΫ90ΓψΘ§ABΘΫ10Θ§ACΘΫ8Θ§ΒψNΈΣBCΒΡ÷–ΒψΘ§Ε·ΒψE”…AΒψ≥ωΖΔΘ§―ΊAB‘ΥΕ·Θ§ΥΌΕ»ΈΣΟΩΟκ5ΗωΒΞΈΜΘ§Ε·ΒψF”…AΒψ≥ωΖΔΘ§―ΊAM‘ΥΕ·Θ§ΥΌΕ»ΈΣΟΩΟκ8ΗωΒΞΈΜΘ§Β±ΒψEΒΫ¥οΒψB ±Θ§ΝΫΒψΆ§ ±ΆΘ÷Ι‘ΥΕ·Θ§ΙΐAΓΔEΓΔFΉςΓ―OΘ°
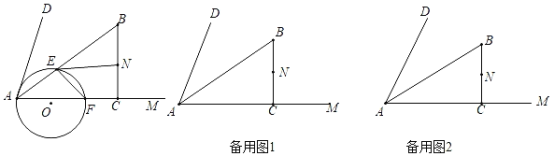
Θ®1Θ©≈–ΕœΓςAEFΒΡ–ΈΉ¥ΈΣΓΓ ΓΓΘ§≤Δ≈–ΕœAD”κΓ―OΒΡΈΜ÷ΟΙΊœΒΈΣΓΓ ΓΓΘΜ
Θ®2Θ©«σtΈΣΚΈ÷Β ±Θ§EN”κΓ―Oœύ«–Θ§«σ≥ω¥Υ ±Γ―OΒΡΑκΨΕΘ§≤Δ±»ΫœΑκΨΕ”κΝ”ΜΓ![]() ≥ΛΕ»ΒΡ¥σ–ΓΘΜ
≥ΛΕ»ΒΡ¥σ–ΓΘΜ
Θ®3Θ©÷±Ϋ”–¥≥ωΓςAEFΒΡΡΎ–Ρ‘ΥΕ·ΒΡ¬ΖΨΕ≥ΛΈΣΓΓ ΓΓΘΜΘ®ΉΔΘΚΒ±AΓΔEΓΔF÷ΊΚœ ±Θ§ΡΎ–ΡΨΆ «AΒψΘ©
Θ®4Θ©÷±Ϋ”–¥≥ωœΏΕΈEN”κΓ―O”–ΝΫΗωΙΪΙ≤Βψ ±Θ§tΒΡ»Γ÷ΒΖΕΈßΈΣΓΓ ΓΓΘ°
Θ®≤ΈΩΦ ΐΨίΘΚsin37ΓψΘΫ![]() Θ§tan37ΓψΘΫ
Θ§tan37ΓψΘΫ![]() Θ§tan74ΓψΓ÷
Θ§tan74ΓψΓ÷![]() Θ§sin74ΓψΓ÷
Θ§sin74ΓψΓ÷![]() Θ§cos74ΓψΓ÷
Θ§cos74ΓψΓ÷![]() Θ©
Θ©
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷Σ![]() ÷–
÷–![]() Βψ
Βψ![]() Ζ÷±π‘Ύ±Ώ
Ζ÷±π‘Ύ±Ώ![]() ΓΔ±Ώ
ΓΔ±Ώ![]() …œΘ§Ν§Ϋ”
…œΘ§Ν§Ϋ”![]() Βψ
Βψ![]() ΓΔΒψ
ΓΔΒψ![]() ‘Ύ÷±œΏ
‘Ύ÷±œΏ![]() Ά§≤ύΘ§Ν§Ϋ”
Ά§≤ύΘ§Ν§Ϋ”![]() «“
«“![]() Θ°
Θ°
Θ®1Θ©Βψ![]() ”κΒψ
”κΒψ![]() ÷ΊΚœ ±Θ§
÷ΊΚœ ±Θ§
ΔΌ»γΆΦ1Θ§![]() ±Θ§
±Θ§![]() ΚΆ
ΚΆ![]() ΒΡ ΐΝΩΙΊœΒ « ΘΜΈΜ÷ΟΙΊœΒ « ΘΜ
ΒΡ ΐΝΩΙΊœΒ « ΘΜΈΜ÷ΟΙΊœΒ « ΘΜ
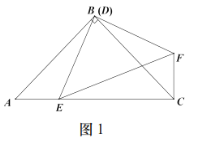
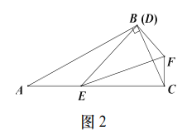
ΔΎ»γΆΦ2Θ§![]() ±Θ§≤¬œκ
±Θ§≤¬œκ![]() ΚΆ
ΚΆ![]() ΒΡΙΊœΒΘ§≤ΔΥΒΟςάμ”…ΘΜ
ΒΡΙΊœΒΘ§≤ΔΥΒΟςάμ”…ΘΜ
Θ®2Θ©![]() ±Θ§
±Θ§
Δέ»γΆΦ3Θ§![]() ±Θ§»τ
±Θ§»τ![]() «σ
«σ![]() ΒΡ≥ΛΕ»ΘΜ
ΒΡ≥ΛΕ»ΘΜ
Δή»γΆΦ4Θ§![]() ±Θ§Βψ
±Θ§Βψ![]() Ζ÷±πΈΣ
Ζ÷±πΈΣ![]() ΚΆ
ΚΆ![]() ΒΡ÷–ΒψΘ§»τ
ΒΡ÷–ΒψΘ§»τ![]() Θ§÷±Ϋ”–¥≥ω
Θ§÷±Ϋ”–¥≥ω![]() ΒΡΉν–Γ÷ΒΘ°
ΒΡΉν–Γ÷ΒΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΙϊ≈ΉΈοœΏmΒΡΕΞΒψ‘Ύ≈ΉΈοœΏn…œΘ§Ά§ ±≈ΉΈοœΏnΒΡΕΞΒψ‘Ύ≈ΉΈοœΏm…œΘ§Ρ«Ο¥Έ“Ο«ΨΆ≥Τ≈ΉΈοœΏm”κnΈΣΫΜ»Ύ≈ΉΈοœΏΘ°
Θ®1Θ©“―÷Σ≈ΉΈοœΏaΘΚ![]() Θ§≈–Εœœ¬Ν–≈ΉΈοœΏbΘΚ
Θ§≈–Εœœ¬Ν–≈ΉΈοœΏbΘΚ![]() Θ§cΘΚ
Θ§cΘΚ![]() ”κ“―÷Σ≈ΉΈοœΏa «ΖώΈΣΫΜ»Ύ≈ΉΈοœΏΘΩ≤ΔΥΒΟςάμ”…ΘΜ
”κ“―÷Σ≈ΉΈοœΏa «ΖώΈΣΫΜ»Ύ≈ΉΈοœΏΘΩ≤ΔΥΒΟςάμ”…ΘΜ
Θ®2Θ©‘Ύ÷±œΏy=2…œ”–“ΜΕ·ΒψPΘ®tΘ§2Θ©Θ§ΫΪ≈ΉΈοœΏaΘΚ![]() »ΤΒψPΘ®tΘ§2Θ©–ΐΉΣ180ΒΟΒΫ≈ΉΈοœΏlΘ§»τ≈ΉΈοœΏa”κlΈΣΫΜ»Ύ≈ΉΈοœΏΘ§«σ≈ΉΈοœΏlΒΡΫβΈω ΫΘΜ
»ΤΒψPΘ®tΘ§2Θ©–ΐΉΣ180ΒΟΒΫ≈ΉΈοœΏlΘ§»τ≈ΉΈοœΏa”κlΈΣΫΜ»Ύ≈ΉΈοœΏΘ§«σ≈ΉΈοœΏlΒΡΫβΈω ΫΘΜ
Θ®3Θ©MΈΣ≈ΉΈοœΏaΘΚ![]() ΒΡΕΞΒψΘ§QΈΣ≈ΉΈοœΏaΒΡΫΜ»Ύ≈ΉΈοœΏΒΡΕΞΒψΘ§ «Ζώ¥φ‘Ύ“‘MQΈΣ–±±ΏΒΡΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈMQSΘ§ Ι÷±Ϋ«ΕΞΒψS‘Ύy÷α…œΘΩ»τ¥φ‘ΎΘ§«σ≥ωΒψSΒΡΉχ±ξΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
ΒΡΕΞΒψΘ§QΈΣ≈ΉΈοœΏaΒΡΫΜ»Ύ≈ΉΈοœΏΒΡΕΞΒψΘ§ «Ζώ¥φ‘Ύ“‘MQΈΣ–±±ΏΒΡΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈMQSΘ§ Ι÷±Ϋ«ΕΞΒψS‘Ύy÷α…œΘΩ»τ¥φ‘ΎΘ§«σ≥ωΒψSΒΡΉχ±ξΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦ,“―÷ΣΓœBAC=30Γψ,Α―ΓςABC»ΤΉ≈ΒψAΥ≥ ±’κ–ΐΉΣΒΫΓςADEΒΡΈΜ÷Ο, ΙΒΟΒψDΘ§AΘ§C‘ΎΆ§“Μ÷±œΏ…œΘ°
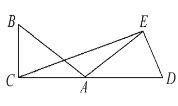
Θ®1Θ©ΓςABC–ΐΉΣΝΥΕύ…ΌΕ»?
Θ®2Θ©Ν§Ϋ”CEΘ§ ‘≈–ΕœΓςAECΒΡ–ΈΉ¥ΘΜ
Θ®3Θ©«σ ΓœAECΒΡΕ» ΐΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥…Χ≥ΓΨΌΑλ≥ιΫ±ΜνΕ·Θ§Ιφ‘ρ»γœ¬ΘΚ‘Ύ≤ΜΆΗΟςΒΡ¥ϋΉ”÷–”–2ΗωΚλ«ρΚΆ2ΗωΚΎ«ρΘ§’β–©«ρ≥ΐ―’…ΪΆβΕΦœύΆ§Θ§ΙΥΩΆΟΩ¥ΈΟΰ≥ω“ΜΗω«ρΘ§»τΟΰΒΫΚλ«ρΘ§‘ρΜώΒΟ1ΖίΫ±ΤΖΘ§»τΟΰΒΫΚΎ«ρΘ§‘ρΟΜ”–Ϋ±ΤΖΓΘ
Θ®1Θ©»γΙϊ–ΓΖΦ÷Μ”–“Μ¥ΈΟΰ«ρΜζΜαΘ§Ρ«Ο¥–ΓΖΦΜώΒΟΫ±ΤΖΒΡΗ≈¬ ΈΣ ΓΓΘΜ
Θ®2Θ©»γΙϊ–ΓΖΦ”–ΝΫ¥ΈΟΰ«ρΜζΜαΘ®Οΰ≥ωΚσ≤ΜΖ≈ΜΊΘ©Θ§«σ–ΓΖΦΜώΒΟ2ΖίΫ±ΤΖΒΡΗ≈¬ ΓΘΘ®«κ”ΟΓΑΜ≠ ςΉ¥ΆΦΓ±ΜρΓΑΝ–±μΓ±Β»ΖΫΖ®–¥≥ωΖ÷ΈωΙΐ≥ΧΘ©
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§Εΰ¥ΈΚ· ΐyΘΫax2+bx+cΒΡΆΦœσ”κy÷α’ΐΑκ÷αœύΫΜΘ§ΤδΕΞΒψΉχ±ξΈΣΘ®![]() Θ§1Θ©Θ§œ¬Ν–Ϋα¬έΘΚΔΌabcΘΦ0ΘΜΔΎa+bΘΫ0ΘΜΔέ4ac©¹b2ΘΫ4aΘΜΔήa+b+cΘΦ0Θ°Τδ÷–’ΐ»ΖΒΡ”–Θ®ΓΓΓΓΘ©ΗωΘ°
Θ§1Θ©Θ§œ¬Ν–Ϋα¬έΘΚΔΌabcΘΦ0ΘΜΔΎa+bΘΫ0ΘΜΔέ4ac©¹b2ΘΫ4aΘΜΔήa+b+cΘΦ0Θ°Τδ÷–’ΐ»ΖΒΡ”–Θ®ΓΓΓΓΘ©ΗωΘ°
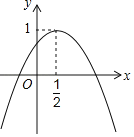
A.1B.2C.3D.4
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§÷±l1ΓΈl2Θ§ΒψAΓΔBΙΧΕ®‘Ύ÷±œΏl2…œΘ§ΒψC «÷±œΏ11…œ“ΜΕ·ΒψΘ§»τΒψEΓΔFΖ÷±πΈΣCAΓΔCB÷–ΒψΘ§Ε‘”Ύœ¬Ν–Ης÷ΒΘΚΔΌœΏΕΈEFΒΡ≥ΛΘΜΔΎΓςCEFΒΡ÷ή≥ΛΘΜΔέΓςCEFΒΡΟφΜΐΘΜΔήΓœECFΒΡΕ» ΐΘ§Τδ÷–≤ΜΥφΒψCΒΡ“ΤΕ·ΕχΗΡ±δΒΡ «Θ®ΓΓΓΓΘ©

A.ΔΌΔΎB.ΔΌΔέC.ΔΎΔήD.ΔέΔή
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com