
【题目】已知![]() 中
中![]() 点
点![]() 分别在边
分别在边![]() 、边
、边![]() 上,连接
上,连接![]() 点
点![]() 、点
、点![]() 在直线
在直线![]() 同侧,连接
同侧,连接![]() 且
且![]() .
.
(1)点![]() 与点
与点![]() 重合时,
重合时,
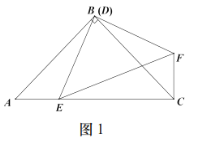
①如图1,![]() 时,
时,![]() 和
和![]() 的数量关系是 ;位置关系是 ;
的数量关系是 ;位置关系是 ;
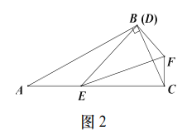
②如图2,![]() 时,猜想
时,猜想![]() 和
和![]() 的关系,并说明理由;
的关系,并说明理由;
(2)![]() 时,
时,
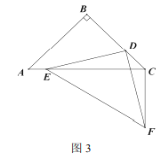
③如图3,![]() 时,若
时,若![]() 求
求![]() 的长度;
的长度;
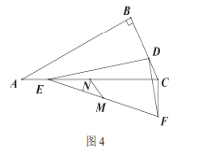
④如图4,![]() 时,点
时,点![]() 分别为
分别为![]() 和
和![]() 的中点,若
的中点,若![]() ,直接写出
,直接写出![]() 的最小值.
的最小值.
【答案】(1)①AE=FC;AE⊥FC;②AE=2FC;AE⊥FC;理由见解析;(2)③FC = 6;④MN的最小值为![]() .
.
【解析】
(1)①利用SAS证出△ABE≌△CDF,从而证出AE=FC,∠A=∠DCF,然后证出∠ACF=90°即可得出结论;
②根据相似三角形的判定证出△ABE∽△CDF,从而得出∠A=∠DCF,![]() ,然后证出∠ACF=90°即可得出结论;
,然后证出∠ACF=90°即可得出结论;
(2)③作GD⊥BC于点D,交AC于点G;作GH⊥AB于点H,交AB于点H;DM⊥AC,利用SAS证出△EDG≌△FDC,从而得出EG=FC,令DC=a,BD=2a,根据三角形的面积公式即可求出a值,从而求出结论;
④连接MD和MC,根据直角三角形斜边上的中线等于斜边的一半可得DM=CM=![]() ,从而得出点M的运动轨迹为是CD的垂直平分线的一部分,作CD的垂直平分线MH交BC于H,然后证出四边形NMHG为平行四边形,从而求出结论.
,从而得出点M的运动轨迹为是CD的垂直平分线的一部分,作CD的垂直平分线MH交BC于H,然后证出四边形NMHG为平行四边形,从而求出结论.
(1)①解:∵![]()
![]()
∴∠ABC=∠EDF=90°,∠A+∠BCA=90°
∴∠ABE+∠EDC=∠CDF+∠EDC
∴∠ABE=∠CDF
∵![]()
∴AB=CB,DE=DF
∴△ABE≌△CDF
∴AE=FC,∠A=∠DCF
∴∠DCF+∠BCA=90°
∴∠ACF=90°
∴AE⊥FC
故答案为:AE=FC;AE⊥FC;
②证明:AE=2FC;AE⊥FC
∵DF⊥DE
∴∠EDF=∠ABC=90°
∴∠ABE=∠CDF·
∵![]()
∴△ABE∽△CDF
∴∠A=∠DCF,![]()
∵∠A+∠ACB=90°
∴∠DCF+∠ACB=90°
∴∠ACF=90°;即FC⊥AE·
(2)③解:作GD⊥BC于点D,交AC于点G;作GH⊥AB于点H,交AB于点H;DM⊥AC.
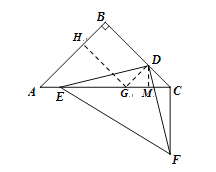
∴四边形BDGH为矩形
∴DB=HG
∵∠ABC=90°,![]()
∴∠A=∠HGA =∠ACB=45°
∴DC=DG
∵DE⊥DF
∴∠EDG=∠FDC
∴△EDG≌△FDC(SAS)
∴EG=FC
∵BD=2CD
∴令DC=a,BD=2a
∴AG=![]()
∴EG=![]() ,MD=
,MD=![]() ·
·
∵![]()
∴![]()
解得![]() ,
,![]() (舍)
(舍)
∴FC = EG=6
④∵![]() ,AB=10
,AB=10
∴BC=5
∵![]()
∴CD=![]()
![]()
由③易证∠ECF=90°
在Rt△EDF和Rt△ECF中,点M为EF的中点,连接MD和MC
∴DM=CM=![]()
∴点M的运动轨迹为是CD的垂直平分线的一部分,作CD的垂直平分线MH交BC于H
∴当NM⊥MH时,MN的最小,易知MN∥BC,MH∥AB,CH=![]() =
=![]()
取BC的中点G,连接NG,则CG=![]() =
=![]()
∴NG为△ABC的中位线
∴NG∥AB
∴MH∥NG
∴四边形NMHG为平行四边形
∴此时MN=GH=CG-CH=![]()
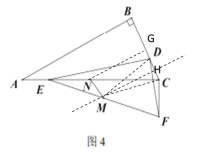
即MN的最小值为![]() .
.


 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案科目:初中数学 来源: 题型:
【题目】受“新冠”疫情的影响,某销售商在网上销售![]() 、
、![]() 两种型号的“手写板”,获利颇丰.已知
两种型号的“手写板”,获利颇丰.已知![]() 型,
型,![]() 型手写板进价、售价和每日销量如表格所示:
型手写板进价、售价和每日销量如表格所示:
进价(元/个) | 售价(元/个) | 销量(个/日) | |
|
|
|
|
|
|
|
|
根据市场行情,该销售商对![]() 型手写板降价销售,同时对
型手写板降价销售,同时对![]() 型手写板提高售价,此时发现
型手写板提高售价,此时发现![]() 型手写板每降低
型手写板每降低![]() 元就可多卖
元就可多卖![]() 个,
个,![]() 型手写板每提高
型手写板每提高![]() 元就少卖
元就少卖![]() 个,要保持每天销售总量不变,设其中
个,要保持每天销售总量不变,设其中![]() 型手写板每天多销售
型手写板每天多销售![]() 个,每天总获利的利润为
个,每天总获利的利润为![]() 元
元
(1)求![]() 与
与![]() 之间的函数关系式并写出
之间的函数关系式并写出![]() 的取值范围;
的取值范围;
(2)要使每天的利润不低于![]() 元,直接写出
元,直接写出![]() 的取值范围;
的取值范围;
(3)该销售商决定每销售一个![]() 型手写板,就捐
型手写板,就捐![]() 元给
元给![]() 因“新冠疫情”影响的困难家庭,当
因“新冠疫情”影响的困难家庭,当![]() 时,每天的最大利润为
时,每天的最大利润为![]() 元,求
元,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠BAC=60°,AD平分∠BAC交边BC于点D,分别过D作DE∥AC交边AB于点E,DF∥AB交边AC于点F.
(1)如图1,试判断四边形AEDF的形状,并说明理由;
(2)如图2,若AD=4![]() ,点H,G分别在线段AE,AF上,且EH=AG=3,连接EG交AD于点M,连接FH交EG于点N.
,点H,G分别在线段AE,AF上,且EH=AG=3,连接EG交AD于点M,连接FH交EG于点N.
(i)求ENEG的值;
(ii)将线段DM绕点D顺时针旋转60°得到线段DM′,求证:H,F,M′三点在同一条直线上
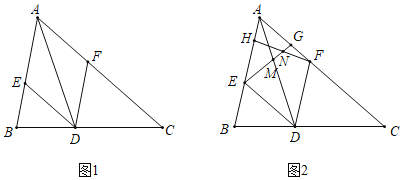
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020贺岁片《囧妈》提档大年三十网络首播.“乐调查”平台为了全面了解观众对《囧妈》的满意度情况,进行随机抽样调查,分为四个类别:![]() .非常满意;
.非常满意;![]() .满意;
.满意;![]() .基本满意;
.基本满意;![]() .不满意,依据调查数据绘制成图1和图2的统计图(不完整).
.不满意,依据调查数据绘制成图1和图2的统计图(不完整).
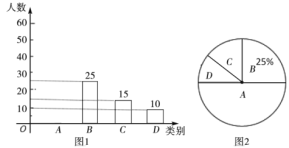
根据以上信息,解答下列问题:
(1)本次接受调查的观众共有_______人;
(2)扇形统计图中,扇形![]() 的圆心角度数是_______;
的圆心角度数是_______;
(3)请补全条形统计图;
(4)“乐调查”平台调查了春节期间观看《固妈》的观众约5000人,请估计观众对该电影的满意(![]() 、
、![]() 、
、![]() 类视为满意)的人数.
类视为满意)的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 是边长为
是边长为![]() 的正方形
的正方形![]() 的对角线
的对角线![]() 上的动点,过点
上的动点,过点![]() 分别作
分别作![]() 于点
于点![]()
![]() 于点
于点![]() ,连接
,连接![]() 并延长,交射线
并延长,交射线![]() 于点
于点![]() 交射线
交射线![]() 于点
于点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() 当
当![]() 点在
点在![]() 上运动时(不包括
上运动时(不包括![]() 两点),以下结论:①
两点),以下结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() 的最小值是
的最小值是![]() .其中正确的是_______.(把你认为正确结论的序号都填上)
.其中正确的是_______.(把你认为正确结论的序号都填上)

查看答案和解析>>
科目:初中数学 来源: 题型:
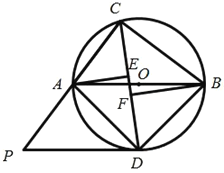
【题目】如图,ABC内接于⊙O,AB为⊙O的直径,∠ACB的平分线CD交⊙O于点D,过点D作⊙O的切线PD,交CA的延长线于点P,过点A作AE⊥CD于点E,过点B作BF⊥CD于点F.
(1)求证:PD//AB;
(2)求证:DE=BF;
(3)若AC=6,tan∠CAB=![]() ,求线段PC的长.
,求线段PC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
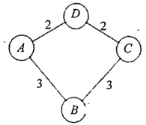
【题目】A,B,C,D四个地区爆发病毒疫情,它们之间的道路连通情况和距离(单位:km)如图所示,经调查发现,某地区受感染率与相邻地区自发病率和距离有关,具体公式为:
A地受B地的感染率![]() .已知A地受B地和D地感染率之相邻地区和为9%,D地的自发病率为24%.
.已知A地受B地和D地感染率之相邻地区和为9%,D地的自发病率为24%.
(1)求B地的自发病率;
(2)规定某地的危险系数等于该地的自发病率与总受感染率的和.
①若C地危险系数是A地危险系数的两倍,且D地受感染率比B地高5%,求A地的自发病率;
②在①的条件下,A地派出6支医疗队支援B,D两地,每派出1支医疗队,A地自身发病率上升0.75%,每支医疗队可以让被支援的地区的自发病率下降4%.在保证A地危险系数不上升的前提下,A地各派往B,D两地多少支队伍时,B地的自发病率下降最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰△ABC中,AB=BC.CD∥AB,点D在点C的右侧,点A,E关于直线BD对称,CE交BD于点F,AE交DB延长线于点G.
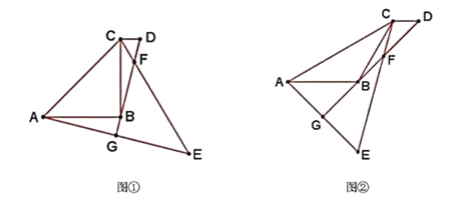
(1)(猜想)
如图①,当∠ABC=90°时,∠EFG=________;
(2)(探究)
在(1)的前提下,若AB=4,CD=1,求EF的长;
(3)(应用)
如图②,当∠ABC=120°时,若EF=2 ![]() ,AB=2,则CD=________.
,AB=2,则CD=________.
查看答案和解析>>
科目:初中数学 来源: 题型:
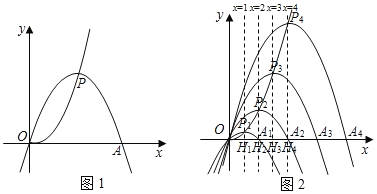
【题目】已知点P为抛物线y![]() x2上一动点,以P为顶点,且经过原点O的抛物线,记作“yp”,设其与x轴另一交点为A,点P的横坐标为m.
x2上一动点,以P为顶点,且经过原点O的抛物线,记作“yp”,设其与x轴另一交点为A,点P的横坐标为m.
(1)①当△OPA为直角三角形时,m= ;
②当△OPA为等边三角形时,求此时“yp”的解析式;
(2)若P点的横坐标分别为1,2,3,…n(n为正整数)时,抛物线“yp”分别记作“![]() ”、“
”、“![]() ”…,“
”…,“![]() ”,设其与x轴另外一交点分别为A1,A2,A3,…An,过P1,P2,P3,…Pn作x轴的垂线,垂足分别为H1,H2,H3,…Hn.
”,设其与x轴另外一交点分别为A1,A2,A3,…An,过P1,P2,P3,…Pn作x轴的垂线,垂足分别为H1,H2,H3,…Hn.
1)① Pn的坐标为 ;OAn= ;(用含n的代数式来表示)
②当PnHn﹣OAn=16时,求n的值.
2)是否存在这样的An,使得∠OP4An=90°,若存在,求n的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com