
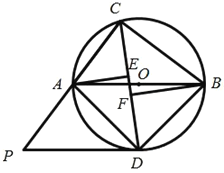
【题目】如图,ABC内接于⊙O,AB为⊙O的直径,∠ACB的平分线CD交⊙O于点D,过点D作⊙O的切线PD,交CA的延长线于点P,过点A作AE⊥CD于点E,过点B作BF⊥CD于点F.
(1)求证:PD//AB;
(2)求证:DE=BF;
(3)若AC=6,tan∠CAB=![]() ,求线段PC的长.
,求线段PC的长.
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】
(1)连结OD,由AB为⊙O的直径,根据圆周角定理得AB为⊙O的直径得∠ACB=90°,再由ACD=∠BCD=45°,则∠DAB=∠ABD=45°,所以△DAB为等腰直角三角形,所以DO⊥AB,根据切线的性质得OD⊥PD,于是可得到DP∥AB;
(2)利用角的关系得出∠FBD=∠EDA,进而得出△FBD≌△EDA,即可得出DE=BF;
(3)在Rt△ACB中,利用AC=6,tan∠CAB=![]() ,可得BC=8,再利用勾股定理得出AB=10,由△DAB为等腰直角三角形,可得AD=5
,可得BC=8,再利用勾股定理得出AB=10,由△DAB为等腰直角三角形,可得AD=5![]() ,由AE⊥CD,得出△ACE为等腰直角三角形,得出AE=CE=3
,由AE⊥CD,得出△ACE为等腰直角三角形,得出AE=CE=3![]() ,在Rt△AED中,可得DE=4
,在Rt△AED中,可得DE=4![]() ,得出CD=7
,得出CD=7![]() ,由角的关系得出△PDA∽△PCD,利用比例式可得出PA=
,由角的关系得出△PDA∽△PCD,利用比例式可得出PA=![]() PD,PC=
PD,PC=![]() PD,由PC=PA+AC,可求得PD=
PD,由PC=PA+AC,可求得PD=![]() ,即可得出PC的值.
,即可得出PC的值.
证明:(1)连结![]() ,如图,
,如图,
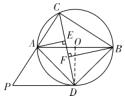
∵![]() 为
为![]() 的直径,∴
的直径,∴![]() ,
,
∵![]() 的平分线交
的平分线交![]() 于点
于点![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 为等腰直角三角形,
为等腰直角三角形,
∴![]() ,
,
∵![]() 为
为![]() 的切线,∴
的切线,∴![]() ,∴
,∴![]() .
.
(2)∵![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴![]() 为等腰直角三角形,∴
为等腰直角三角形,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
在![]() 和
和![]() 中,
中, ,
,
∴![]() ,
,
∴![]() .
.
(3)在![]() ,∵
,∵![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∵![]() 为等腰直角三角形,∴
为等腰直角三角形,∴![]() ,
,
∵![]() ,
,
∴![]() 为等腰直角三角形,∴
为等腰直角三角形,∴![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,
,
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
又∵![]() ,
,
∴![]() ,解得
,解得![]() ,
,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】某校为了解九年级学生新冠疫情防控期间每天居家体育活动的时间(单位:![]() ),在网上随机调查了该校九年级部分学生.根据调查结果,绘制出如下的统计图1和图2.请根据相关信息,解答下列问题:
),在网上随机调查了该校九年级部分学生.根据调查结果,绘制出如下的统计图1和图2.请根据相关信息,解答下列问题:
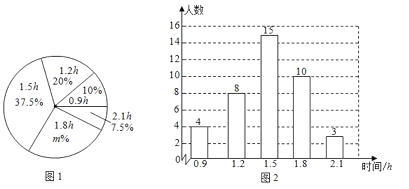
(1)本次接受调查的初中学生人数为________,图①中![]() 的值为________;
的值为________;
(2)这组数据的平均数是________,众数是________,中位数是________;
(3)根据统计的这组每天居家体育活动时间的样本数据,估计该校500名九年级学生居家期间每天体育活动时间大于![]() 的学生人数.
的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,AB为⊙O的直径,D为![]() 的中点,过D作DF⊥AB于点E,交⊙O于点F,交弦BC于点G,连接CD,BF.
的中点,过D作DF⊥AB于点E,交⊙O于点F,交弦BC于点G,连接CD,BF.
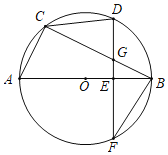
(1)求证:△BFG≌△DCG;
(2)若AC=10,BE=8,求BF的长;
(3)在(2)的条件下,P为⊙O上一点,连接BP,CP,弦CP交直径AB于点H,若△BPH与△CPB相似,求CP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图1,四边形![]() 是正方形,
是正方形,![]() 分别在边
分别在边![]() 、
、![]() 上,且
上,且![]() ,我们把这种模型称为“半角模型”,在解决“半角模型”问题时,旋转是一种常用的方法.
,我们把这种模型称为“半角模型”,在解决“半角模型”问题时,旋转是一种常用的方法.
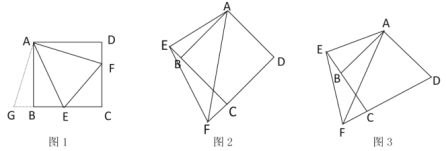
(1)在图l中,连接![]() ,为了证明结论“
,为了证明结论“![]() ”,小亮将
”,小亮将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 后解答了这个问题,请按小亮的思路写出证明过程;
后解答了这个问题,请按小亮的思路写出证明过程;
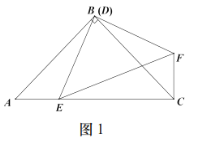
(2)如图2,当![]() 绕点
绕点![]() 旋转到图2位置时,试探究
旋转到图2位置时,试探究![]() 与
与![]() 、
、![]() 之间有怎样的数量关系?
之间有怎样的数量关系?
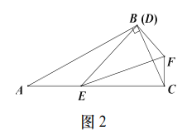
(3)如图3,如果四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 中
中![]() 点
点![]() 分别在边
分别在边![]() 、边
、边![]() 上,连接
上,连接![]() 点
点![]() 、点
、点![]() 在直线
在直线![]() 同侧,连接
同侧,连接![]() 且
且![]() .
.
(1)点![]() 与点
与点![]() 重合时,
重合时,
①如图1,![]() 时,
时,![]() 和
和![]() 的数量关系是 ;位置关系是 ;
的数量关系是 ;位置关系是 ;
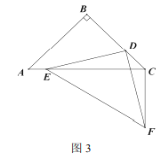
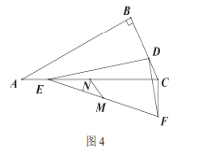
②如图2,![]() 时,猜想
时,猜想![]() 和
和![]() 的关系,并说明理由;
的关系,并说明理由;
(2)![]() 时,
时,
③如图3,![]() 时,若
时,若![]() 求
求![]() 的长度;
的长度;
④如图4,![]() 时,点
时,点![]() 分别为
分别为![]() 和
和![]() 的中点,若
的中点,若![]() ,直接写出
,直接写出![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司销售部有营业员20人,该公司为了调动营业员的积极性,决定实行目标管理,根据目标完成的情况对营业员进行适当的奖励,为了确定一个适当的月销售目标,公司有关部门统计了这20人某月的销售量,如下表所示:
某公司20位营业员月销售目标统计表
月销售量/件数 | 1760 | 480 | 220 | 180 | 120 | 90 |
人数 | 1 | 1 | 3 | 5 | 6 | 4 |
请根据以上提供的信息解答下列问题:
(1)求这个月中20位营业员的月销售量的平均数;
(2)为了提高大多数营业员积极性,公司将发放A,B,C三个等级的奖金(金额:![]() ),如果你是管理者,从平均数,中位数,众数的角度进行分析,你将如何确定领取A,B,C级奖金各需达到的月销售量.
),如果你是管理者,从平均数,中位数,众数的角度进行分析,你将如何确定领取A,B,C级奖金各需达到的月销售量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠BAC=30°,把△ABC绕着点A顺时针旋转到△ADE的位置,使得点D,A,C在同一直线上.
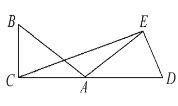
(1)△ABC旋转了多少度?
(2)连接CE,试判断△AEC的形状;
(3)求 ∠AEC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
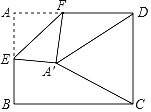
【题目】如图,在矩形纸片ABCD中,AB=4,BC=4![]() ,点E是AB的中点,点F是AD边上的一个动点,将△AEF沿EF所在直线翻折,得到△A'EF,连接A'C,A'D,则当△A'DC是以A'D为腰的等腰三角形时,FD的长是_____.
,点E是AB的中点,点F是AD边上的一个动点,将△AEF沿EF所在直线翻折,得到△A'EF,连接A'C,A'D,则当△A'DC是以A'D为腰的等腰三角形时,FD的长是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某网店专售一款电动牙刷,其成本为20元/支,销售中发现,该商品每天的销售量y(支)与销售单价x(元/支)之间存在如图所示的关系.
(1)求y与x之间的函数关系式.
(2)由于湖北省武汉市爆发了新型冠状病毒肺炎(简称“新冠肺炎”)疫情,该网店店主决定从每天获得的利润中抽出200元捐献给武汉,为了保证捐款后每天剩余利润不低于550元,如何确定这款电动牙刷的销售单价?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com