
【题目】某公司销售部有营业员20人,该公司为了调动营业员的积极性,决定实行目标管理,根据目标完成的情况对营业员进行适当的奖励,为了确定一个适当的月销售目标,公司有关部门统计了这20人某月的销售量,如下表所示:
某公司20位营业员月销售目标统计表
月销售量/件数 | 1760 | 480 | 220 | 180 | 120 | 90 |
人数 | 1 | 1 | 3 | 5 | 6 | 4 |
请根据以上提供的信息解答下列问题:
(1)求这个月中20位营业员的月销售量的平均数;
(2)为了提高大多数营业员积极性,公司将发放A,B,C三个等级的奖金(金额:![]() ),如果你是管理者,从平均数,中位数,众数的角度进行分析,你将如何确定领取A,B,C级奖金各需达到的月销售量.
),如果你是管理者,从平均数,中位数,众数的角度进行分析,你将如何确定领取A,B,C级奖金各需达到的月销售量.
科目:初中数学 来源: 题型:
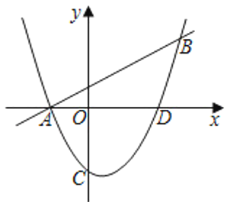
【题目】如图,一次函数y=![]() x+1的图象与二次函数y=
x+1的图象与二次函数y=![]() x2+bx+c的图象交于A,B两点,点A在x轴上.点B的横坐标为4.
x2+bx+c的图象交于A,B两点,点A在x轴上.点B的横坐标为4.
(1)b= ,c= ;
(2)设二次函数的图象与y轴交于C点,与x轴的另一个交点为D.连接AC,CD,求∠ACD的正弦值;
(3)若M点在x轴下方二次函数图象上,
①过M点作y轴平行线交直线AB于点E,以M点为圆心,ME的长为半径画圆,求圆M在直线AB上截得的弦长的最大值;
②若∠ABM=∠ACO,则点M的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有甲乙两个玩具小汽车在笔直的240米跑道![]() 上进行折返跑游戏,甲从点
上进行折返跑游戏,甲从点![]() 出发,匀速在
出发,匀速在![]() 、
、![]() 之间折返跑,同时乙从点
之间折返跑,同时乙从点![]() 出发,以大于甲的速度匀速在
出发,以大于甲的速度匀速在![]() 、
、![]() 之间折返跑.在折返点的时间忽略不计.
之间折返跑.在折返点的时间忽略不计.

(1)若甲的速度为![]() ,乙的速度为
,乙的速度为![]() ,第一次迎面相遇的时间为
,第一次迎面相遇的时间为![]() ,则
,则![]() 与
与![]() 的关系式___________;
的关系式___________;
(注释:当两车相向而行时相遇是迎面相遇,当两车在![]() 点相遇时也视为迎面相遇)
点相遇时也视为迎面相遇)
(2)如图1,
①若甲乙两车在距![]() 点20米处第一次迎面相遇,则他们在距
点20米处第一次迎面相遇,则他们在距![]() 点_______米第二次迎面相遇:
点_______米第二次迎面相遇:
②若甲乙两车在距![]() 点50米处第一次迎面相遇,则他们在距
点50米处第一次迎面相遇,则他们在距![]() 点__________米第二次迎面相遇;
点__________米第二次迎面相遇;
(3)设甲乙两车在距![]() 点
点![]() 米处第一次迎面相遇,在距
米处第一次迎面相遇,在距![]() 点
点![]() 米处第二次迎面相遇.某同学发现了
米处第二次迎面相遇.某同学发现了![]() 与
与![]() 的函数关系,并画出了部分函数图象(线段
的函数关系,并画出了部分函数图象(线段![]() ,不包括点
,不包括点![]() ,如图2所示).
,如图2所示).
①则![]() _______,并在图2中补全
_______,并在图2中补全![]() 与
与![]() 的函数图象(在图中注明关键点的数据);
的函数图象(在图中注明关键点的数据);
②分别求出各部分图象对应的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】文化是一个国家、一个民族的灵魂,近年来,央视推出《中国诗词大会》、《中国成语大会》、《朗读者》、《经曲咏流传》等一系列文化栏目.为了解学生对这些栏目的喜爱情况,某学校组织学生会成员随机抽取了部分学生进行调查,被调查的学生必须从《经曲咏流传》(记为A)、《中国诗词大会》(记为B)、《中国成语大会》(记为C)、《朗读者》(记为D)中选择自己最喜爱的一个栏目,也可以不选以上四类而写出一个自己最喜爱的其他文化栏目(这时记为E).根据调查结果绘制成如图所示的两幅不完整的统计图.
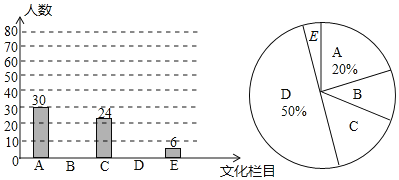
请根据图中信息解答下列问题:
(1)在这项调查中,共调查了 名学生;
(2)最喜爱《朗读者》的学生有 名;
(3)扇形统计图中“B”所在扇形圆心角的度数为 ;
(4)选择“E”的学生中有2名女生,其余为男生,现从选择“E”的学生中随机选出两名学生参加座谈,请直接写出:刚好选到一名男生和一名女生的概率为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
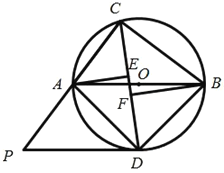
【题目】如图,ABC内接于⊙O,AB为⊙O的直径,∠ACB的平分线CD交⊙O于点D,过点D作⊙O的切线PD,交CA的延长线于点P,过点A作AE⊥CD于点E,过点B作BF⊥CD于点F.
(1)求证:PD//AB;
(2)求证:DE=BF;
(3)若AC=6,tan∠CAB=![]() ,求线段PC的长.
,求线段PC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
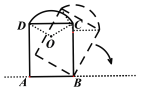
【题目】如图,竖直放置的一个铝合金窗框由矩形和弧形两部分组成,AB=![]() m,AD= 2m,弧CD所对的圆心角为∠COD=120°.现将窗框绕点B顺时针旋转横放在水平的地面上,这一过程中,窗框上的点到地面的最大高度为__m.
m,AD= 2m,弧CD所对的圆心角为∠COD=120°.现将窗框绕点B顺时针旋转横放在水平的地面上,这一过程中,窗框上的点到地面的最大高度为__m.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A在反比例函数![]() (x<0)的图象上,连接OA,分别以点O和点A为圆心,大于
(x<0)的图象上,连接OA,分别以点O和点A为圆心,大于![]() 的长为半径作弧,两弧相交于B,C两点,过B,C两点作直线交x轴于点D,连接AD.若∠AOD=30°,△AOD的面积为2,则k的值为( )
的长为半径作弧,两弧相交于B,C两点,过B,C两点作直线交x轴于点D,连接AD.若∠AOD=30°,△AOD的面积为2,则k的值为( )
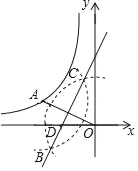
A.﹣6B.6C.﹣2D.﹣3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习《圆》这一单元时,我们学习了圆周角定理的推论:圆内接四边形的对角互补;事实上,它的逆命题:对角互补的四边形的四个顶点共圆,也是一个真命题.在图形旋转的综合题中经常会出现对角互补的四边形,那么,我们就可以借助“对角互补的四边形的四个顶点共圆”,然后借助圆的相关知识来解决问题,例如:
已知:![]() 是等边三角形,点
是等边三角形,点![]() 是
是![]() 内一点,连接
内一点,连接![]() ,将线段
,将线段![]() 绕
绕![]() 逆时针旋转
逆时针旋转![]() 得到线段
得到线段![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,并延长
,并延长![]() 交
交![]() 于点
于点![]() .当点
.当点![]() 在如图所示的位置时:
在如图所示的位置时:
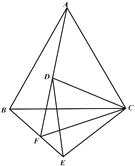
(1)观察填空:
①与![]() 全等的三角形是________;
全等的三角形是________;
②![]() 的度数为
的度数为
(2)利用题干中的结论,证明:![]() ,
,![]() ,
,![]() ,
,![]() 四点共圆;
四点共圆;
(3)直接写出线段![]() ,
,![]() ,
,![]() 之间的数量关系.____________________.
之间的数量关系.____________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
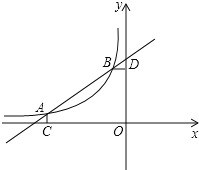
【题目】如图,已知A(﹣3,![]() ),B(﹣1,m)是一次函数y=kx+b与反比例函数y=
),B(﹣1,m)是一次函数y=kx+b与反比例函数y=![]() 图象的两个交点,AC⊥x轴于点C,BD⊥y轴于点D.
图象的两个交点,AC⊥x轴于点C,BD⊥y轴于点D.
(1)求m的值及一次函数解析式;
(2)P是线段AB上的一点,连接PC,PD,若△PCA和△PDB面积相等,求点P坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com