
【题目】已知如图1,四边形![]() 是正方形,
是正方形,![]() 分别在边
分别在边![]() 、
、![]() 上,且
上,且![]() ,我们把这种模型称为“半角模型”,在解决“半角模型”问题时,旋转是一种常用的方法.
,我们把这种模型称为“半角模型”,在解决“半角模型”问题时,旋转是一种常用的方法.
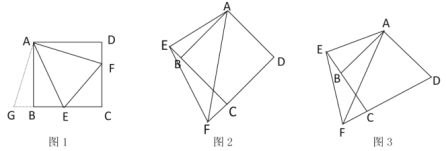
(1)在图l中,连接![]() ,为了证明结论“
,为了证明结论“![]() ”,小亮将
”,小亮将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 后解答了这个问题,请按小亮的思路写出证明过程;
后解答了这个问题,请按小亮的思路写出证明过程;
(2)如图2,当![]() 绕点
绕点![]() 旋转到图2位置时,试探究
旋转到图2位置时,试探究![]() 与
与![]() 、
、![]() 之间有怎样的数量关系?
之间有怎样的数量关系?
(3)如图3,如果四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1)见解析;(2)![]() ,见解析;(3)
,见解析;(3)![]() 的长为5.
的长为5.
【解析】
(1)利用旋转的性质和正方形的性质,证明![]() 即可求证;
即可求证;
(2)在![]() 上取一点
上取一点![]() ,使
,使![]() ,先证明
,先证明![]() ,再证明
,再证明![]() ,即可得出答案;
,即可得出答案;
(3)在![]() 上取一点
上取一点![]() ,使
,使![]() ,先证明
,先证明![]() ,再证明
,再证明![]() ,得到EF=FG,设
,得到EF=FG,设![]() ,用含x的代数式表达GC和EF,根据勾股定理列出方程,解出x的值即可.
,用含x的代数式表达GC和EF,根据勾股定理列出方程,解出x的值即可.
(1)证明:∵![]() ,
,
∴![]() ,
,![]() ,
,
∵∠EAF=45°,
∴∠DAF+∠BAE=45°,即∠GAB+∠BAE=45°,
∴∠GAE=∠EAF,
∴在△GAE和△FAE中 ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
(2)解:在![]() 上取一点
上取一点![]() ,使
,使![]() ,
,
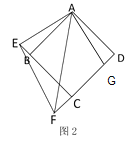 ,
,
∵四边形ABCD是正方形,
∴AD=AB,∠ADG=∠ABE=90°,
又∵DG=BE,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∵∠EAF=∠BAE+∠BAF=45°,
∴∠GAD+∠BAF=45°,
∴∠GAF=45°,即∠EAF=∠GAF,
∴![]() ,
,
∴![]() ,
,
即![]() ;
;
(3)解:在![]() 上取一点
上取一点![]() ,使
,使![]() ,
,
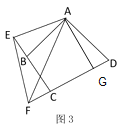
∵![]() ,
,
∴∠D+∠ABC=180°,
∵∠ABE+∠ABC=180°,
∴∠D=∠ABE,
又∵AB=AD,DG=BE,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∵∠EAF=∠BAE+∠BAF=45°,
∴∠GAD+∠BAF=45°,
∴∠GAF=45°,即∠EAF=∠GAF,
∴![]() ,
,
∴EF=FG
设![]()
∴![]() ,
,
∴![]()
在![]() 中,
中,![]()
∴![]() ,
,
解得:![]() ,
,
答:![]() 的长为5.
的长为5.


科目:初中数学 来源: 题型:
【题目】二次函数![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,
两点,![]() ,与直线
,与直线![]() 交于
交于![]() 、
、![]() 两点,点
两点,点![]() 在
在![]() 轴上,
轴上,![]() .
.
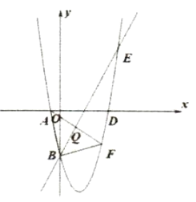
(1)求二次函数的解析式;
(2)在抛物线上有一点![]() ,若
,若![]() 的面积为
的面积为![]() ,求点
,求点![]() 的横坐标;
的横坐标;
(3)点![]() 在第四象限的抛物线上运动,连接
在第四象限的抛物线上运动,连接![]() ,与直线
,与直线![]() 交于点
交于点![]() ,连接
,连接![]() ,
,![]() .设
.设![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
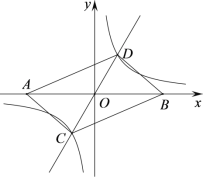
【题目】如图,在平面直角坐标系中,点A的坐标为(m,0),m<0,点B与点A 关于原点对称,直线![]() 与双曲线
与双曲线![]() 交于C,D两点.
交于C,D两点.
(1)直接判断后填空:四边形ACBD的形状一定是 ;
(2)若点D(1,t),求双曲线的解析式;
(3)在(2)的前提下,四边形ACBD为矩形时,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有甲乙两个玩具小汽车在笔直的240米跑道![]() 上进行折返跑游戏,甲从点
上进行折返跑游戏,甲从点![]() 出发,匀速在
出发,匀速在![]() 、
、![]() 之间折返跑,同时乙从点
之间折返跑,同时乙从点![]() 出发,以大于甲的速度匀速在
出发,以大于甲的速度匀速在![]() 、
、![]() 之间折返跑.在折返点的时间忽略不计.
之间折返跑.在折返点的时间忽略不计.

(1)若甲的速度为![]() ,乙的速度为
,乙的速度为![]() ,第一次迎面相遇的时间为
,第一次迎面相遇的时间为![]() ,则
,则![]() 与
与![]() 的关系式___________;
的关系式___________;
(注释:当两车相向而行时相遇是迎面相遇,当两车在![]() 点相遇时也视为迎面相遇)
点相遇时也视为迎面相遇)
(2)如图1,
①若甲乙两车在距![]() 点20米处第一次迎面相遇,则他们在距
点20米处第一次迎面相遇,则他们在距![]() 点_______米第二次迎面相遇:
点_______米第二次迎面相遇:
②若甲乙两车在距![]() 点50米处第一次迎面相遇,则他们在距
点50米处第一次迎面相遇,则他们在距![]() 点__________米第二次迎面相遇;
点__________米第二次迎面相遇;
(3)设甲乙两车在距![]() 点
点![]() 米处第一次迎面相遇,在距
米处第一次迎面相遇,在距![]() 点
点![]() 米处第二次迎面相遇.某同学发现了
米处第二次迎面相遇.某同学发现了![]() 与
与![]() 的函数关系,并画出了部分函数图象(线段
的函数关系,并画出了部分函数图象(线段![]() ,不包括点
,不包括点![]() ,如图2所示).
,如图2所示).
①则![]() _______,并在图2中补全
_______,并在图2中补全![]() 与
与![]() 的函数图象(在图中注明关键点的数据);
的函数图象(在图中注明关键点的数据);
②分别求出各部分图象对应的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
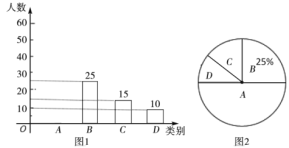
【题目】2020贺岁片《囧妈》提档大年三十网络首播.“乐调查”平台为了全面了解观众对《囧妈》的满意度情况,进行随机抽样调查,分为四个类别:![]() .非常满意;
.非常满意;![]() .满意;
.满意;![]() .基本满意;
.基本满意;![]() .不满意,依据调查数据绘制成图1和图2的统计图(不完整).
.不满意,依据调查数据绘制成图1和图2的统计图(不完整).
根据以上信息,解答下列问题:
(1)本次接受调查的观众共有_______人;
(2)扇形统计图中,扇形![]() 的圆心角度数是_______;
的圆心角度数是_______;
(3)请补全条形统计图;
(4)“乐调查”平台调查了春节期间观看《固妈》的观众约5000人,请估计观众对该电影的满意(![]() 、
、![]() 、
、![]() 类视为满意)的人数.
类视为满意)的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】文化是一个国家、一个民族的灵魂,近年来,央视推出《中国诗词大会》、《中国成语大会》、《朗读者》、《经曲咏流传》等一系列文化栏目.为了解学生对这些栏目的喜爱情况,某学校组织学生会成员随机抽取了部分学生进行调查,被调查的学生必须从《经曲咏流传》(记为A)、《中国诗词大会》(记为B)、《中国成语大会》(记为C)、《朗读者》(记为D)中选择自己最喜爱的一个栏目,也可以不选以上四类而写出一个自己最喜爱的其他文化栏目(这时记为E).根据调查结果绘制成如图所示的两幅不完整的统计图.
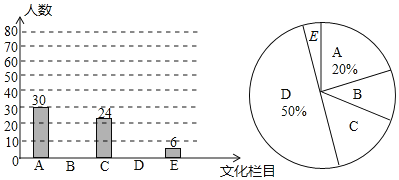
请根据图中信息解答下列问题:
(1)在这项调查中,共调查了 名学生;
(2)最喜爱《朗读者》的学生有 名;
(3)扇形统计图中“B”所在扇形圆心角的度数为 ;
(4)选择“E”的学生中有2名女生,其余为男生,现从选择“E”的学生中随机选出两名学生参加座谈,请直接写出:刚好选到一名男生和一名女生的概率为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
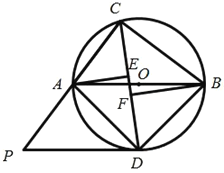
【题目】如图,ABC内接于⊙O,AB为⊙O的直径,∠ACB的平分线CD交⊙O于点D,过点D作⊙O的切线PD,交CA的延长线于点P,过点A作AE⊥CD于点E,过点B作BF⊥CD于点F.
(1)求证:PD//AB;
(2)求证:DE=BF;
(3)若AC=6,tan∠CAB=![]() ,求线段PC的长.
,求线段PC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A在反比例函数![]() (x<0)的图象上,连接OA,分别以点O和点A为圆心,大于
(x<0)的图象上,连接OA,分别以点O和点A为圆心,大于![]() 的长为半径作弧,两弧相交于B,C两点,过B,C两点作直线交x轴于点D,连接AD.若∠AOD=30°,△AOD的面积为2,则k的值为( )
的长为半径作弧,两弧相交于B,C两点,过B,C两点作直线交x轴于点D,连接AD.若∠AOD=30°,△AOD的面积为2,则k的值为( )
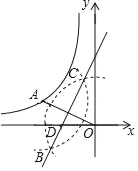
A.﹣6B.6C.﹣2D.﹣3
查看答案和解析>>
科目:初中数学 来源: 题型:
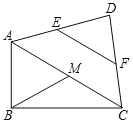
【题目】(1)化简:(2x+1)(2x﹣1)+(x+1)(1﹣2x).
(2)如图,在四边形ABCD中,AB⊥BC,E,F,M分别是AD,DC,AC的中点,连接EF,BM,求证:EF=BM.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com