
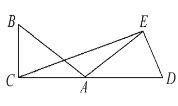
【题目】如图,在等腰△ABC中,AB=BC.CD∥AB,点D在点C的右侧,点A,E关于直线BD对称,CE交BD于点F,AE交DB延长线于点G.
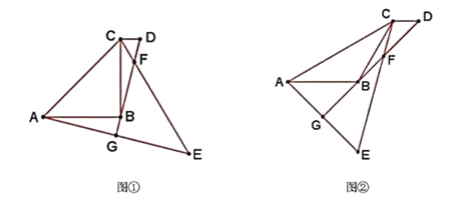
(1)(猜想)
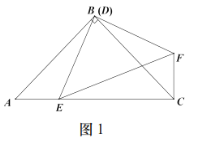
如图①,当∠ABC=90°时,∠EFG=________;
(2)(探究)
在(1)的前提下,若AB=4,CD=1,求EF的长;
(3)(应用)
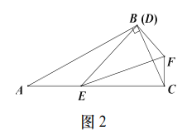
如图②,当∠ABC=120°时,若EF=2 ![]() ,AB=2,则CD=________.
,AB=2,则CD=________.
【答案】(1)45°;(2)EF= ![]() ;(3)
;(3)![]() -1
-1
【解析】
(1)连接BE,利用轴对称的性质得BE=BC=AB,然后利用等腰三角形的性质以及三角形内角、外角关系求解即可;
(2)易证△ABG∽△BCD,利用相似三角形的性质得AG:BC=AB:BD,据此求出AG.由轴对称性得GE=AG,由∠EFG=45°得EF=![]() AG,计算即可得到答案;
AG,计算即可得到答案;
(3)连接BE,过点C作CH⊥GD于H,同(1)可得∠BEF=∠BCE=∠CBF=15°,进而得BF=CF=![]() ,则CH=
,则CH=![]() ,进而得CD=
,进而得CD=![]() CH,故可求.
CH,故可求.
(1)连接BE,如图所示:
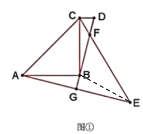
因为点A,E关于直线BD对称,且AB=BC,所以利用轴对称的性质得BE=BC=AB,且![]() .由等腰三角形的性质可得
.由等腰三角形的性质可得![]() ,
,![]() ,又因为三角形ACE的内角等于
,又因为三角形ACE的内角等于![]() ,且∠ABC=90°,AB=BC,所以三角形ACE的内角等于
,且∠ABC=90°,AB=BC,所以三角形ACE的内角等于![]() ,所以
,所以![]() ,又因为
,又因为![]() ,所以
,所以![]() ,又因为
,又因为![]() ,所以∠EFG=45°.
,所以∠EFG=45°.
(2)解:∵CD∥AB,∴∠D=∠ABG.
又∠AGB=∠BCD=∠ABC=90°,
∴△ABG∽△BCD,
又∵AB=4,CD=1,AB=BC,
∴BD=![]() ,AB=BC=4,
,AB=BC=4,
∴AG:BC=AB:BD,可以得到AG= ![]() .由对称性,得GE=AG=
.由对称性,得GE=AG= ![]() .又由∠EFG=45°得EF=
.又由∠EFG=45°得EF=![]() AG,∴EF
AG,∴EF![]() =
= ![]() .
.
(3)连接BE,过点C作CH⊥GD于H,如下图所示:
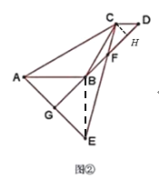
同(1)可得∠BEF=∠BCE=∠CBF=15°,进而得BF=CF=![]() ,则CH=
,则CH=![]() ,进而得CD=
,进而得CD=![]() CH,故可求CD=
CH,故可求CD=![]() =
=![]() -1.
-1.


科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,点E为对角线AC上一点,且AE![]() CB,连接DE并延长交BC于点G,过点A作AH⊥BE于点H,交BC于点F.以下结论:①BH
CB,连接DE并延长交BC于点G,过点A作AH⊥BE于点H,交BC于点F.以下结论:①BH![]() HE;②∠BEG
HE;②∠BEG![]() 45°;③△ABF ≌△DCG; ④4BH2
45°;③△ABF ≌△DCG; ④4BH2![]() BG·CD.其中正确结论的个数是( )
BG·CD.其中正确结论的个数是( )
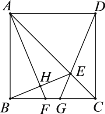
A.1个B.2
C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 中
中![]() 点
点![]() 分别在边
分别在边![]() 、边
、边![]() 上,连接
上,连接![]() 点
点![]() 、点
、点![]() 在直线
在直线![]() 同侧,连接
同侧,连接![]() 且
且![]() .
.
(1)点![]() 与点
与点![]() 重合时,
重合时,
①如图1,![]() 时,
时,![]() 和
和![]() 的数量关系是 ;位置关系是 ;
的数量关系是 ;位置关系是 ;
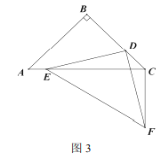
②如图2,![]() 时,猜想
时,猜想![]() 和
和![]() 的关系,并说明理由;
的关系,并说明理由;
(2)![]() 时,
时,
③如图3,![]() 时,若
时,若![]() 求
求![]() 的长度;
的长度;
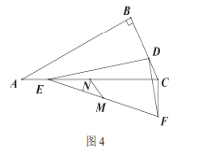
④如图4,![]() 时,点
时,点![]() 分别为
分别为![]() 和
和![]() 的中点,若
的中点,若![]() ,直接写出
,直接写出![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠BAC=30°,把△ABC绕着点A顺时针旋转到△ADE的位置,使得点D,A,C在同一直线上.
(1)△ABC旋转了多少度?
(2)连接CE,试判断△AEC的形状;
(3)求 ∠AEC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场举办抽奖活动,规则如下:在不透明的袋子中有2个红球和2个黑球,这些球除颜色外都相同,顾客每次摸出一个球,若摸到红球,则获得1份奖品,若摸到黑球,则没有奖品。
(1)如果小芳只有一次摸球机会,那么小芳获得奖品的概率为 ;
(2)如果小芳有两次摸球机会(摸出后不放回),求小芳获得2份奖品的概率。(请用“画树状图”或“列表”等方法写出分析过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
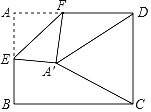
【题目】如图,在矩形纸片ABCD中,AB=4,BC=4![]() ,点E是AB的中点,点F是AD边上的一个动点,将△AEF沿EF所在直线翻折,得到△A'EF,连接A'C,A'D,则当△A'DC是以A'D为腰的等腰三角形时,FD的长是_____.
,点E是AB的中点,点F是AD边上的一个动点,将△AEF沿EF所在直线翻折,得到△A'EF,连接A'C,A'D,则当△A'DC是以A'D为腰的等腰三角形时,FD的长是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象与y轴正半轴相交,其顶点坐标为(![]() ,1),下列结论:①abc<0;②a+b=0;③4ac﹣b2=4a;④a+b+c<0.其中正确的有( )个.
,1),下列结论:①abc<0;②a+b=0;③4ac﹣b2=4a;④a+b+c<0.其中正确的有( )个.
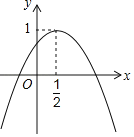
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为鼓励大学毕业生自主创业,某市政府出台了相关政策:由政府协调,本市企业按成本价提供产品给大学毕业生自主销售,成本价与出厂价之间的差价由政府承担.李明按照相关政策投资销售本市生产的一种新型节能灯.已知这种节能灯的成本价为每件8元,出厂价为每件10元,每月销售量y(件)与销售单价x(元)之间的关系近似满足一次函数:y=-10x+500.
(1)李明在开始创业的第一个月将销售单价定为20元,那么政府这个月为他承担的总差价为多少元?
(2)设李明获得的利润为w(元),当销售单价定为多少元时,每月可获得最大利润?
(3)物价部门规定,这种节能灯的销售单价不得高于25元.如果李明想要每月获得的利润不低于3410元,那么政府为他承担的总差价最少为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】深圳某百果园店售卖赣南脐橙,已知每千克脐橙的成本价为![]() 元,在销售脐橙的这
元,在销售脐橙的这![]() 天时间内,销售单价
天时间内,销售单价![]() (元/千克)与时间第
(元/千克)与时间第![]() (天)之间的函数关系式为
(天)之间的函数关系式为![]() (
(![]() ,且
,且![]() 为整数),日销售量
为整数),日销售量![]() (千克)与时间第
(千克)与时间第![]() (天)之间的函数关系式为
(天)之间的函数关系式为![]() (
(![]() ,且
,且![]() 为整数)
为整数)
(1)请你直接写出日销售利润![]() (元)与时间第
(元)与时间第![]() (天)之间的函数关系式;
(天)之间的函数关系式;
(2)该店有多少天日销售利润不低于![]() 元?
元?
(3)在实际销售中,该店决定每销售![]() 千克脐橙,就捐赠
千克脐橙,就捐赠![]() 元给希望工程,在这
元给希望工程,在这![]() 天中,每天扣除捐赠后的日销售利润随时间
天中,每天扣除捐赠后的日销售利润随时间![]() 的增大而增大,求
的增大而增大,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com