
ЁОЬтФПЁПШчЭМЃЌдкЁЯDAMФкВПзіRtЁїABCЃЌABЦНЗжЁЯDAMЃЌЁЯACBЃН90ЁуЃЌABЃН10ЃЌACЃН8ЃЌЕуNЮЊBCЕФжаЕуЃЌЖЏЕуEгЩAЕуГіЗЂЃЌбиABдЫЖЏЃЌЫйЖШЮЊУПУы5ИіЕЅЮЛЃЌЖЏЕуFгЩAЕуГіЗЂЃЌбиAMдЫЖЏЃЌЫйЖШЮЊУПУы8ИіЕЅЮЛЃЌЕБЕуEЕНДяЕуBЪБЃЌСНЕуЭЌЪБЭЃжЙдЫЖЏЃЌЙ§AЁЂEЁЂFзїЁбOЃЎ
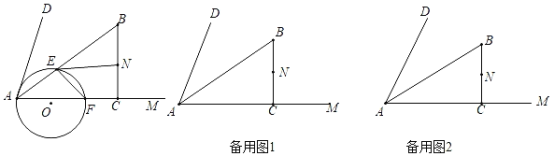
ЃЈ1ЃЉХаЖЯЁїAEFЕФаЮзДЮЊЁЁ ЁЁЃЌВЂХаЖЯADгыЁбOЕФЮЛжУЙиЯЕЮЊЁЁ ЁЁЃЛ
ЃЈ2ЃЉЧѓtЮЊКЮжЕЪБЃЌENгыЁбOЯрЧаЃЌЧѓГіДЫЪБЁбOЕФАыОЖЃЌВЂБШНЯАыОЖгыСгЛЁ![]() ГЄЖШЕФДѓаЁЃЛ
ГЄЖШЕФДѓаЁЃЛ
ЃЈ3ЃЉжБНгаДГіЁїAEFЕФФкаФдЫЖЏЕФТЗОЖГЄЮЊЁЁ ЁЁЃЛЃЈзЂЃКЕБAЁЂEЁЂFжиКЯЪБЃЌФкаФОЭЪЧAЕуЃЉ
ЃЈ4ЃЉжБНгаДГіЯпЖЮENгыЁбOгаСНИіЙЋЙВЕуЪБЃЌtЕФШЁжЕЗЖЮЇЮЊЁЁ ЁЁЃЎ
ЃЈВЮПМЪ§ОнЃКsin37ЁуЃН![]() ЃЌtan37ЁуЃН
ЃЌtan37ЁуЃН![]() ЃЌtan74ЁуЁж
ЃЌtan74ЁуЁж![]() ЃЌsin74ЁуЁж
ЃЌsin74ЁуЁж![]() ЃЌcos74ЁуЁж
ЃЌcos74ЁуЁж![]() ЃЉ
ЃЉ
ЁОД№АИЁПЃЈ1ЃЉЕШбќШ§НЧаЮЃЌЯрЧаЃЛЃЈ2ЃЉt=1ЃЌАыОЖЮЊ![]() ЃЌСгЛЁ
ЃЌСгЛЁ![]() ГЄЖШДѓгкАыОЖЃЛЃЈ3ЃЉ
ГЄЖШДѓгкАыОЖЃЛЃЈ3ЃЉ![]() ЃЛЃЈ4ЃЉ1ЁмtЁм
ЃЛЃЈ4ЃЉ1ЁмtЁм![]()
ЁОНтЮіЁП
ЃЈ1ЃЉЙ§ЕуEзїEHЁЭAFгкHЃЌСЌНгOAЁЂOEЁЂOHЃЌгЩЙДЙЩЖЈРэЧѓГіBCЃН![]() ЃН6ЃЌЩшдЫЖЏЪБМфЮЊtЃЌдђAEЃН5tЃЌAFЃН8tЃЌжЄУїЁїEAHЁзЁїBACЃЌЕУГі
ЃН6ЃЌЩшдЫЖЏЪБМфЮЊtЃЌдђAEЃН5tЃЌAFЃН8tЃЌжЄУїЁїEAHЁзЁїBACЃЌЕУГі![]() ЃЌЧѓГіAHЃН4tЃЌдђFHЃНAFЉAHЃН4tЃЌAHЃНFHЃЌЕУГіЁїAEFЪЧЕШбќШ§НЧаЮЃЌжЄУїEЁЂHЁЂOШ§ЕуЙВЯпЃЌЕУГіЁЯOAF+ЁЯAOEЃН90ЁуЃЌгЩABЦНЗжЁЯDAMЃЌЕУГіЁЯDAEЃНЁЯEAFЃНЁЯEFAЃЌгЩдВжмНЧЖЈРэЕУГіЁЯAOEЃН2ЁЯEFAЃЌдђЁЯDAF+ЁЯOAFЃН90ЁуЃНЁЯDAOЃЌМДOAЁЭADЃЌМДПЩЕУГіADгыЁбOЯрЧаЃЛ
ЃЌЧѓГіAHЃН4tЃЌдђFHЃНAFЉAHЃН4tЃЌAHЃНFHЃЌЕУГіЁїAEFЪЧЕШбќШ§НЧаЮЃЌжЄУїEЁЂHЁЂOШ§ЕуЙВЯпЃЌЕУГіЁЯOAF+ЁЯAOEЃН90ЁуЃЌгЩABЦНЗжЁЯDAMЃЌЕУГіЁЯDAEЃНЁЯEAFЃНЁЯEFAЃЌгЩдВжмНЧЖЈРэЕУГіЁЯAOEЃН2ЁЯEFAЃЌдђЁЯDAF+ЁЯOAFЃН90ЁуЃНЁЯDAOЃЌМДOAЁЭADЃЌМДПЩЕУГіADгыЁбOЯрЧаЃЛ
ЃЈ2ЃЉСЌНгOAЁЂOFЁЂOEЃЌOEгкACНЛгкHЃЌвзжЄЫФБпаЮEHCNЮЊОиаЮЃЌЕУГіEHЃНNCЃЌгЩЙДЙЩЖЈРэЕУГіEHЃН![]() ЃН3tЃЌдђNCЃН3tЃЌBCЃН2NCЃН6tЃЌгЩBCЃН6ЃЌЕУГіtЃН1ЃЌдђAHЃН4ЃЌEHЃН3ЃЌЩшЁбOЕФАыОЖЮЊxЃЌдђOHЃНxЉ3ЃЌгЩЙДЙЩЖЈРэЕУГіOA2ЃНOH2+AH2ЃЌНтЕУxЃН
ЃН3tЃЌдђNCЃН3tЃЌBCЃН2NCЃН6tЃЌгЩBCЃН6ЃЌЕУГіtЃН1ЃЌдђAHЃН4ЃЌEHЃН3ЃЌЩшЁбOЕФАыОЖЮЊxЃЌдђOHЃНxЉ3ЃЌгЩЙДЙЩЖЈРэЕУГіOA2ЃНOH2+AH2ЃЌНтЕУxЃН![]() ЃЌЕУГіOHЃН
ЃЌЕУГіOHЃН![]() ЃЌtanЁЯAOHЃН
ЃЌtanЁЯAOHЃН![]() ЃЌЕУГіЁЯAOHЃН74ЁуЃЌгЩЁЯAOHЃН60ЁуЪБЃЌЁїAOEЪЧЕШБпШ§НЧаЮЃЌAEЃНOAЃЌ74ЁуЃО60ЁуЃЌЕУГіAEЃОOAЃЌдђСгЛЁ
ЃЌЕУГіЁЯAOHЃН74ЁуЃЌгЩЁЯAOHЃН60ЁуЪБЃЌЁїAOEЪЧЕШБпШ§НЧаЮЃЌAEЃНOAЃЌ74ЁуЃО60ЁуЃЌЕУГіAEЃОOAЃЌдђСгЛЁ![]() ГЄЖШЕФДѓгкАыОЖЃЛ
ГЄЖШЕФДѓгкАыОЖЃЛ
ЃЈ3ЃЉЕБЕуEдЫЖЏЕНBЕуЪБЃЌtЃН2ЃЌAFЃН16ЃЌAEЃНEFЃНABЃН10ЃЌДЫЪБЁїAEFЕФФкаФМЧЮЊGЃЌЕБAЁЂEЁЂFжиКЯЪБЃЌФкаФЮЊAЕуЃЌЁїAEFЕФФкаФдЫЖЏЕФТЗОЖГЄЮЊAGЃЌзїGPЁЭAEгкPЃЌGQЁЭEFгкQЃЌСЌНгAGЁЂGFЃЌдђCGЃНPGЃНNQЃЌSЁїAEFЃН![]() AFBCЃН48ЃЌЩшCGЃНPGЃНNQЃНaЃЌдђSЁїAEFЃНSЁїAGF+SЁїAEB+SЁїFEGЃН
AFBCЃН48ЃЌЩшCGЃНPGЃНNQЃНaЃЌдђSЁїAEFЃНSЁїAGF+SЁїAEB+SЁїFEGЃН![]() AFCG+
AFCG+![]() AEPG+
AEPG+![]() EFNQЃН
EFNQЃН![]() ЁС(16+10+10)aЃН48ЃЌНтЕУaЃН
ЁС(16+10+10)aЃН48ЃЌНтЕУaЃН![]() ЃЌгЩЙДЙЩЖЈРэЕУГіAC2+CG2ЃНAG2ЃЌЕУГіAGЃН
ЃЌгЩЙДЙЩЖЈРэЕУГіAC2+CG2ЃНAG2ЃЌЕУГіAGЃН![]() ЃЛ
ЃЛ
ЃЈ4ЃЉЗжБ№ЬжТлСНжжМЋЯоЮЛжУЃЌЂйЕБENгыЁбOЯрЧаЪБЃЌгЩЃЈ2ЃЉжЊЃЌtЃН1ЃЛЂкЕБNдкЁбOЩЯЃЌМДONЮЊЁбOЕФАыОЖЃЌСЌНгOAЁЂONЁЂOEЃЌOEНЛACгкHЃЌЙ§ЕуOзїOKЁЭBCгкKЃЌдђЫФБпаЮOKCHЮЊОиаЮЃЌOAЃНOEЃНONЃЌЕУГіOHЃНCKЃЌAHЃН4tЃЌEHЃН3tЃЌЩшЁбOЕФАыОЖЮЊxЃЌгЩЙДЙЩЖЈРэЕУГіAH2+OH2ЃНOA2ЃЌНтЕУxЃН![]() tЃЌдђOHЃНCKЃН
tЃЌдђOHЃНCKЃН![]() tЃЌгЩЙДЙЩЖЈРэЕУГі
tЃЌгЩЙДЙЩЖЈРэЕУГі![]() ЃЌНтЕУtЃН
ЃЌНтЕУtЃН![]() ЃЌМДПЩЕУГіНсЙћЃЎ
ЃЌМДПЩЕУГіНсЙћЃЎ
ЃЈ1ЃЉЙ§ЕуEзїEHЁЭAFгкHЃЌСЌНгOAЁЂOEЁЂOHЃЌШчЭМ1ЫљЪОЃК
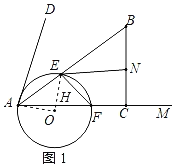
ЁпЁЯACBЃН90ЁуЃЌABЃН10ЃЌACЃН8ЃЌ
ЁрBCЃН![]() ЃН6ЃЌ
ЃН6ЃЌ
ЩшдЫЖЏЪБМфЮЊtЃЌдђAEЃН5tЃЌAFЃН8tЃЌ
ЁпЁЯAHEЃНЁЯACBЃН90ЁуЃЌЁЯEAHЃНЁЯBACЃЌ
ЁрЁїEAHЁзЁїBACЃЌ
Ёр![]() ЃЌМД
ЃЌМД![]() ЃЌ
ЃЌ
ЁрAHЃН4tЃЌ
ЁрFHЃНAFЉAHЃН8tЉ4tЃН4tЃЌ
ЁрAHЃНFHЃЌ
ЁпEHЁЭAFЃЌ
ЁрЁїAEFЪЧЕШбќШ§НЧаЮЃЌ
ЁрEЮЊ![]() ЕФжаЕуЃЌЁЯEAFЃНЁЯEFAЃЌ
ЕФжаЕуЃЌЁЯEAFЃНЁЯEFAЃЌ
ЁпAHЃНFHЃЌ
ЁрOHЁЭACЃЌ
ЁрEЁЂHЁЂOШ§ЕуЙВЯпЃЌ
ЁрЁЯOAF+ЁЯAOEЃН90ЁуЃЌ
ЁпABЦНЗжЁЯDAMЃЌ
ЁрЁЯDAEЃНЁЯEAFЃНЁЯEFAЃЌ
ЁпЁЯAOEЃН2ЁЯEFAЃЌ
ЁрЁЯAOEЃНЁЯDAE+ЁЯEAFЃНЁЯDAFЃЌ
ЁрЁЯDAF+ЁЯOAFЃН90ЁуЃНЁЯDAOЃЌМДOAЁЭADЃЌ
ЁпOAЮЊЁбOЕФАыОЖЃЌ
ЁрADгыЁбOЯрЧаЃЛ
ЙЪД№АИЮЊЃКЕШбќШ§НЧаЮЃЌЯрЧаЃЛ
ЃЈ2ЃЉСЌНгOA
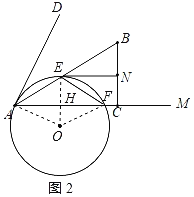
гЩЃЈ1ЃЉжЊЃКEHЁЭACЃЌ
ЁпENгыЁбOЯрЧаЃЌ
ЁрЁЯOENЃН90ЁуЃЌ
ЁпЁЯACBЃН90ЁуЃЌ
ЁрЫФБпаЮEHCNЮЊОиаЮЃЌ
ЁрEHЃНNCЃЌ
дкRtЁїAHEжаЃЌEHЃН![]() ЃН3tЃЌ
ЃН3tЃЌ
ЁрNCЃН3tЃЌ
ЁпЕуNЮЊBCЕФжаЕуЃЌ
ЁрBCЃН2NCЃН6tЃЌ
ЁпBCЃН6ЃЌ
Ёр6tЃН6ЃЌ
ЁрtЃН1ЃЌ
ЁрAHЃН4ЃЌEHЃН3ЃЌ
ЩшЁбOЕФАыОЖЮЊxЃЌдђOHЃНxЉ3ЃЌ
дкRtЁїAOHжаЃЌгЩЙДЙЩЖЈРэЕУЃКOA2ЃНOH2+AH2ЃЌМДx2ЃН(xЉ3)2+42ЃЌ
НтЕУЃКxЃН![]() ЃЌ
ЃЌ
ЁрЁбOЕФАыОЖЮЊ![]() ЃЌ
ЃЌ
ЁрOHЃН![]() ЃЌ
ЃЌ
ЁрtanЁЯAOHЃН![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁрЁЯAOHЃН74ЁуЃЌ
ЁпЁЯAOHЃН60ЁуЪБЃЌЁїAOEЪЧЕШБпШ§НЧаЮЃЌAEЃНOAЃЌ74ЁуЃО60ЁуЃЌ
ЁрAEЃОOAЃЌ
ЁрСгЛЁ![]() ГЄЖШЕФДѓгкАыОЖЃЛ
ГЄЖШЕФДѓгкАыОЖЃЛ
ЃЈ3ЃЉЕБЕуEдЫЖЏЕНBЕуЪБЃЌtЃН10ЁТ5ЃН2ЃЌ
ЁрAFЃН2ЁС8ЃН16ЃЌAEЃНEFЃНABЃН10ЃЌ
ДЫЪБЁїAEFЕФФкаФМЧЮЊGЃЌЕБAЁЂEЁЂFжиКЯЪБЃЌФкаФЮЊAЕуЃЌ
ЁрЁїAEFЕФФкаФдЫЖЏЕФТЗОЖГЄЮЊAGЃЌ
зїGPЁЭAEгкPЃЌGQЁЭEFгкQЃЌСЌНгAGЁЂGFЃЌдђCGЃНPGЃНNQЃЌШчЭМ3ЫљЪОЃК
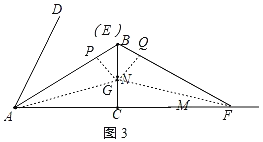
SЁїAEFЃН![]() AFBCЃН
AFBCЃН![]() ЁС16ЁС6ЃН48ЃЌ
ЁС16ЁС6ЃН48ЃЌ
ЩшCGЃНPGЃНNQЃНaЃЌ
дђSЁїAEFЃНSЁїAGF+SЁїAEB+SЁїFEGЃН![]() AFCG+
AFCG+![]() AEPG+
AEPG+![]() EFNQЃН
EFNQЃН![]() ЁС(16+10+10)aЃН48ЃЌ
ЁС(16+10+10)aЃН48ЃЌ
НтЕУЃКaЃН![]() ЃЌ
ЃЌ
дкRtЁїAGCжаЃЌAC2+CG2ЃНAG2ЃЌМД82+(![]() )2ЃНAGЃЌ
)2ЃНAGЃЌ
ЁрAGЃН![]() ЃЌ
ЃЌ
ЙЪД№АИЮЊЃК![]() ЃЛ
ЃЛ
ЃЈ4ЃЉЗжБ№ЬжТлСНжжМЋЯоЮЛжУЃЌ
ЂйЕБENгыЁбOЯрЧаЪБЃЌгЩЃЈ2ЃЉжЊЃЌtЃН1ЃЛ
ЂкЕБNдкЁбOЩЯЃЌМДONЮЊЁбOЕФАыОЖЃЌ
СЌНгOAЁЂONЁЂOEЃЌOEНЛACгкHЃЌЙ§ЕуOзїOKЁЭBCгкKЃЌШчЭМ4ЫљЪОЃК
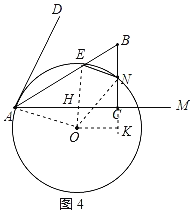
дђЫФБпаЮOKCHЮЊОиаЮЃЌOAЃНOEЃНONЃЌ
ЁрOHЃНCKЃЌAHЃН4tЃЌEHЃН3tЃЌ
ЩшЁбOЕФАыОЖЮЊxЃЌ
дђдкRtЁїAOHжаЃЌAH2+OH2ЃНOA2ЃЌМД(4t)2+(xЉ3t)2ЃНx2ЃЌ
НтЕУЃКxЃН![]() tЃЌ
tЃЌ
ЁрOHЃНCKЃН![]() tЉ3tЃН
tЉ3tЃН![]() tЃЌ
tЃЌ
дкRtЁїOKNжаЃЌOK2+KN2ЃНON2ЃЌМД(8Љ4t)2+(3+![]() t)2ЃН(
t)2ЃН(![]() t)2ЃЌ
t)2ЃЌ
НтЕУЃКtЃН![]() ЃЌ
ЃЌ
ЁрЯпЖЮENгыЁбOгаСНИіЙЋЙВЕуЪБЃЌtЕФШЁжЕЗЖЮЇЮЊЃК1ЁмtЁм![]() ЃЌ
ЃЌ
ЙЪД№АИЮЊЃК1ЁмtЁм![]() ЃЎ
ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаЫЕЗЈВЛе§ШЗЕФЪЧЃЈ ЃЉ
A.ЮЊСЫНтШЋЪажааЁбЇЩњЖдЭјТчжБВЅПЮЕФТњвтГЬЖШЃЌгІВЩгУГщбљЕїВщ
B.Ъ§Он![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЕФЗНВюЮЊ
ЕФЗНВюЮЊ![]()
C.Ш§НЧаЮЕФЕФФкаФЕНШ§НЧаЮШ§БпОрРыЯрЕШ
D.ЫГДЮСЌНгЖдНЧЯпДЙжБЕФЫФБпаЮЕФжаЕуЃЌЫљаЮГЩЕФЫФБпаЮЮЊСтаЮ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊЬсЩ§бЇЩњЕФвеЪѕЫибјЃЌбЇаЃМЦЛЎПЊЩшЫФУХвеЪѕбЁаоПЮЃКAЃЎЪщЗЈЃЛBЃЎЛцЛЃЛCЃЎРжЦїЃЛDЃЎЮшЕИЃЎЮЊСЫНтбЇЩњЖдЫФУХЙІПЮЕФЯВЛЖЧщПіЃЌдкШЋаЃЗЖЮЇФкЫцЛњГщШЁШєИЩУћбЇЩњНјааЮЪОэЕїВщЃЈУПИіБЛЕїВщЕФбЇЩњБиаыбЁдёЖјЧвжЛФмбЁдёЦфжавЛУХЃЉЃЎНЋЪ§ОнНјааећРэЃЌВЂЛцжЦГЩШчЯТСНЗљВЛЭъећЕФЭГМЦЭМЃЌЧыНсКЯЭМжаЫљИјаХЯЂНтД№ЯТСаЮЪЬтЃК
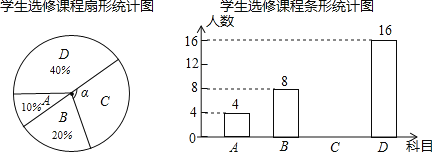
ЃЈ1ЃЉБОДЮЕїВщЕФбЇЩњЙВгаЖрЩйШЫЃПЩШаЮЭГМЦЭМжаЁЯІСЕФЖШЪ§ЪЧЖрЩйЃП
ЃЈ2ЃЉЧыАбЬѕаЮЭГМЦЭМВЙГфЭъећЃЛ
ЃЈ3ЃЉбЇаЃЮЊОйАь2018ФъЖШаЃдАЮФЛЏвеЪѕНкЃЌОіЖЈДгAЃЎЪщЗЈЃЛBЃЎЛцЛЃЛCЃЎРжЦїЃЛDЃЎЮшЕИЫФЯювеЪѕаЮЪНжабЁдёЦфжаСНЯюзщГЩвЛИіаТЕФНкФПаЮЪНЃЌЧыгУСаБэЗЈЛђЪїзДЭМЧѓГібЁжаЪщЗЈгыРжЦїзщКЯдквЛЦ№ЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
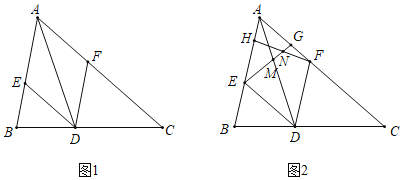
ЁОЬтФПЁПдкЁїABCжаЃЌЁЯBAC=60ЁуЃЌADЦНЗжЁЯBACНЛБпBCгкЕуDЃЌЗжБ№Й§DзїDEЁЮACНЛБпABгкЕуEЃЌDFЁЮABНЛБпACгкЕуFЃЎ
(1)ШчЭМ1ЃЌЪдХаЖЯЫФБпаЮAEDFЕФаЮзДЃЌВЂЫЕУїРэгЩЃЛ
(2)ШчЭМ2ЃЌШєAD=4![]() ЃЌЕуHЃЌGЗжБ№дкЯпЖЮAEЃЌAFЩЯЃЌЧвEH=AG=3ЃЌСЌНгEGНЛADгкЕуMЃЌСЌНгFHНЛEGгкЕуNЃЎ
ЃЌЕуHЃЌGЗжБ№дкЯпЖЮAEЃЌAFЩЯЃЌЧвEH=AG=3ЃЌСЌНгEGНЛADгкЕуMЃЌСЌНгFHНЛEGгкЕуNЃЎ
(i)ЧѓENEGЕФжЕЃЛ
(ii)НЋЯпЖЮDMШЦЕуDЫГЪБеыа§зЊ60ЁуЕУЕНЯпЖЮDMЁфЃЌЧѓжЄЃКHЃЌFЃЌMЁфШ§ЕудкЭЌвЛЬѕжБЯпЩЯ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПНтУмЪ§бЇФЇЪѕЃКФЇЪѕЪІЧыЙлжкаФЯывЛИіЪ§ЃЌШЛКѓНЋетИіЪ§АДвдЯТВНжшВйзїЃК
![]()
ФЇЪѕЪІФмСЂПЬЫЕГіЙлжкЯыЕФФЧИіЪ§ЃЎ
ЃЈ1ЃЉШчЙћаЁСсЯыЕФЪ§ЪЧ![]() ЃЌЧыФуЭЈЙ§МЦЫуАяжњЫ§ИцЫпФЇЪѕЪІЕФНсЙћЃЛ
ЃЌЧыФуЭЈЙ§МЦЫуАяжњЫ§ИцЫпФЇЪѕЪІЕФНсЙћЃЛ
ЃЈ2ЃЉШчЙћаЁУїЯыСЫвЛИіЪ§МЦЫуКѓЃЌИцЫпФЇЪѕЪІНсЙћЮЊ85ЃЌФЧУДФЇЪѕЪІСЂПЬЫЕГіаЁУїЯыЕФФЧИіЪ§ЪЧЃК__________ЃЛ
ЃЈ3ЃЉЙлжкгжНјааСЫМИДЮГЂЪдЃЌФЇЪѕЪІЖМФмСЂПЬЫЕГіЫћУЧЯыЕФФЧИіЪ§ЃЎШєЩшЙлжкаФЯыЕФЪ§ЮЊ![]() ЃЌЧыФуАДееФЇЪѕЪІвЊЧѓЕФдЫЫуЙ§ГЬСаДњЪ§ЪНВЂЛЏМђЃЌдйгУвЛОфЛАЫЕГіетИіФЇЪѕЕФАТУюЃЎ
ЃЌЧыФуАДееФЇЪѕЪІвЊЧѓЕФдЫЫуЙ§ГЬСаДњЪ§ЪНВЂЛЏМђЃЌдйгУвЛОфЛАЫЕГіетИіФЇЪѕЕФАТУюЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП2020КиЫъЦЌЁЖхТшЁЗЬсЕЕДѓФъШ§ЪЎЭјТчЪзВЅ.ЁАРжЕїВщЁБЦНЬЈЮЊСЫШЋУцСЫНтЙлжкЖдЁЖхТшЁЗЕФТњвтЖШЧщПіЃЌНјааЫцЛњГщбљЕїВщЃЌЗжЮЊЫФИіРрБ№ЃК![]() .ЗЧГЃТњвтЃЛ
.ЗЧГЃТњвтЃЛ![]() .ТњвтЃЛ
.ТњвтЃЛ![]() .ЛљБОТњвтЃЛ
.ЛљБОТњвтЃЛ![]() .ВЛТњвтЃЌвРОнЕїВщЪ§ОнЛцжЦГЩЭМ1КЭЭМ2ЕФЭГМЦЭМЃЈВЛЭъећЃЉЃЎ
.ВЛТњвтЃЌвРОнЕїВщЪ§ОнЛцжЦГЩЭМ1КЭЭМ2ЕФЭГМЦЭМЃЈВЛЭъећЃЉЃЎ
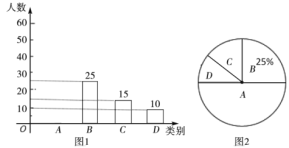
ИљОнвдЩЯаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉБОДЮНгЪмЕїВщЕФЙлжкЙВга_______ШЫЃЛ
ЃЈ2ЃЉЩШаЮЭГМЦЭМжаЃЌЩШаЮ![]() ЕФдВаФНЧЖШЪ§ЪЧ_______ЃЛ
ЕФдВаФНЧЖШЪ§ЪЧ_______ЃЛ
ЃЈ3ЃЉЧыВЙШЋЬѕаЮЭГМЦЭМЃЛ
ЃЈ4ЃЉЁАРжЕїВщЁБЦНЬЈЕїВщСЫДКНкЦкМфЙлПДЁЖЙЬТшЁЗЕФЙлжкдМ5000ШЫЃЌЧыЙРМЦЙлжкЖдИУЕчгАЕФТњвтЃЈ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() РрЪгЮЊТњвтЃЉЕФШЫЪ§ЃЎ
РрЪгЮЊТњвтЃЉЕФШЫЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЕу![]() ЪЧБпГЄЮЊ
ЪЧБпГЄЮЊ![]() ЕФе§ЗНаЮ
ЕФе§ЗНаЮ![]() ЕФЖдНЧЯп
ЕФЖдНЧЯп![]() ЩЯЕФЖЏЕуЃЌЙ§Еу
ЩЯЕФЖЏЕуЃЌЙ§Еу![]() ЗжБ№зї
ЗжБ№зї![]() гкЕу
гкЕу![]()
![]() гкЕу
гкЕу![]() ЃЌСЌНг
ЃЌСЌНг![]() ВЂбгГЄЃЌНЛЩфЯп
ВЂбгГЄЃЌНЛЩфЯп![]() гкЕу
гкЕу![]() НЛЩфЯп
НЛЩфЯп![]() гкЕу
гкЕу![]() ЃЌСЌНг
ЃЌСЌНг![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЕБ
ЕБ![]() Еудк
Еудк![]() ЩЯдЫЖЏЪБ(ВЛАќРЈ
ЩЯдЫЖЏЪБ(ВЛАќРЈ![]() СНЕу)ЃЌвдЯТНсТлЃКЂй
СНЕу)ЃЌвдЯТНсТлЃКЂй![]() ЃЛЂк
ЃЛЂк![]() ЃЛЂл
ЃЛЂл![]() ЃЛЂм
ЃЛЂм![]() ЕФзюаЁжЕЪЧ
ЕФзюаЁжЕЪЧ![]() ЃЎЦфжае§ШЗЕФЪЧ_______ЃЎ(АбФуШЯЮЊе§ШЗНсТлЕФађКХЖМЬюЩЯ)
ЃЎЦфжае§ШЗЕФЪЧ_______ЃЎ(АбФуШЯЮЊе§ШЗНсТлЕФађКХЖМЬюЩЯ)

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПAЃЌBЃЌCЃЌDЫФИіЕиЧјБЌЗЂВЁЖОвпЧщЃЌЫќУЧжЎМфЕФЕРТЗСЌЭЈЧщПіКЭОрРыЃЈЕЅЮЛЃКkmЃЉШчЭМЫљЪОЃЌОЕїВщЗЂЯжЃЌФГЕиЧјЪмИаШОТЪгыЯрСкЕиЧјздЗЂВЁТЪКЭОрРыгаЙиЃЌОпЬхЙЋЪНЮЊЃК
AЕиЪмBЕиЕФИаШОТЪ![]() ЃЎвбжЊAЕиЪмBЕиКЭDЕиИаШОТЪжЎЯрСкЕиЧјКЭЮЊ9%ЃЌDЕиЕФздЗЂВЁТЪЮЊ24%ЃЎ
ЃЎвбжЊAЕиЪмBЕиКЭDЕиИаШОТЪжЎЯрСкЕиЧјКЭЮЊ9%ЃЌDЕиЕФздЗЂВЁТЪЮЊ24%ЃЎ
ЃЈ1ЃЉЧѓBЕиЕФздЗЂВЁТЪЃЛ
ЃЈ2ЃЉЙцЖЈФГЕиЕФЮЃЯеЯЕЪ§ЕШгкИУЕиЕФздЗЂВЁТЪгызмЪмИаШОТЪЕФКЭЃЎ
ЂйШєCЕиЮЃЯеЯЕЪ§ЪЧAЕиЮЃЯеЯЕЪ§ЕФСНБЖЃЌЧвDЕиЪмИаШОТЪБШBЕиИп5%ЃЌЧѓAЕиЕФздЗЂВЁТЪЃЛ
ЂкдкЂйЕФЬѕМўЯТЃЌAЕиХЩГі6жЇвНСЦЖгжЇдЎBЃЌDСНЕиЃЌУПХЩГі1жЇвНСЦЖгЃЌAЕиздЩэЗЂВЁТЪЩЯЩ§0ЃЎ75%ЃЌУПжЇвНСЦЖгПЩвдШУБЛжЇдЎЕФЕиЧјЕФздЗЂВЁТЪЯТНЕ4%ЃЎдкБЃжЄAЕиЮЃЯеЯЕЪ§ВЛЩЯЩ§ЕФЧАЬсЯТЃЌAЕиИїХЩЭљBЃЌDСНЕиЖрЩйжЇЖгЮщЪБЃЌBЕиЕФздЗЂВЁТЪЯТНЕзюЖрЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЁбOжажБОЖЮЊ4ЃЌЯвABЃН2![]() ЃЌЕуCЪЧдВЩЯВЛЭЌгкAЁЂBЕФЕуЃЌФЧУДЁЯACBЖШЪ§ЮЊ_____ЃЎ
ЃЌЕуCЪЧдВЩЯВЛЭЌгкAЁЂBЕФЕуЃЌФЧУДЁЯACBЖШЪ§ЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com