
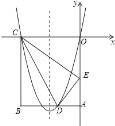
【题目】如图,在矩形OABC中,OA=5,AB=4,点D为边AB上一点,将△BCD沿直线CD折叠,使点B恰好落在边OA上的点E处,分别以OC,OA所在的直线为x轴,y轴建立平面直角坐标系.
(1)求OE的长及经过O,D,C三点抛物线的解析式;
(2)一动点P从点C出发,沿CB以每秒2个单位长度的速度向点B运动,同时动点Q从E点出发,沿EC以每秒1个单位长度的速度向点C运动,当点P到达点B时,两点同时停止运动,设运动时间为t秒,当t为何值时,DP=DQ;
(3)若点N在(1)中抛物线的对称轴上,点M在抛物线上,是否存在这样的点M与点N,使M,N,C,E为顶点的四边形是平行四边形?若存在,请求出M点坐标;若不存在,请说明理由.
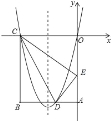
【答案】(1)抛物线解析式为y=x(x+4)=x2+x;
【解析】
试题分析:(1)由折叠的性质可求得CE、CO,在Rt△COE中,由勾股定理可求得OE,设AD=m,在Rt△ADE中,由勾股定理可求得m的值,可求得D点坐标,结合C、O两点,利用待定系数法可求得抛物线解析式;
(2)用t表示出CP、BP的长,可证明△DBP≌△DEQ,可得到BP=EQ,可求得t的值;
(3)可设出N点坐标,分三种情况①EN为对角线,②EM为对角线,③EC为对角线,根据平行四边形的性质可求得对角线的交点横坐标,从而可求得M点的横坐标,再代入抛物线解析式可求得M点的坐标.
试题解析:(1)∵CE=CB=5,CO=AB=4,
∴在Rt△COE中,OE=![]() =3,
=3,
设AD=m,则DE=BD=4﹣m,∵OE=3,∴AE=5﹣3=2,
在Rt△ADE中,由勾股定理可得AD2+AE2=DE2,即m2+22=(4﹣m)2,解得m=![]() ,
,
∴D(﹣![]() ,﹣5),∵C(﹣4,0),O(0,0),∴设过O、D、C三点的抛物线为y=ax(x+4),
,﹣5),∵C(﹣4,0),O(0,0),∴设过O、D、C三点的抛物线为y=ax(x+4),
∴﹣5=﹣![]() a(﹣
a(﹣![]() +4),解得a=
+4),解得a=![]() ,∴抛物线解析式为y=
,∴抛物线解析式为y=![]() x(x+4)=
x(x+4)=![]() x2+
x2+![]() x;
x;
(2)∵CP=2t,∴BP=5﹣2t,∵BD=![]() ,DE=
,DE=![]() =
=![]() ,∴BD=DE,
,∴BD=DE,
在Rt△DBP和Rt△DEQ中,![]() ,∴Rt△DBP≌Rt△DEQ(HL),
,∴Rt△DBP≌Rt△DEQ(HL),
∴BP=EQ,∴5﹣2t=t,∴t=![]() ;
;
(3)∵抛物线的对称轴为直线x=﹣2,∴设N(﹣2,n),
又由题意可知C(﹣4,0),E(0,﹣3),设M(m,y),
①当EN为对角线,即四边形ECNM是平行四边形时,
则线段EN的中点横坐标为![]() =﹣1,线段CM中点横坐标为
=﹣1,线段CM中点横坐标为![]() ,∵EN,CM互相平分,∴
,∵EN,CM互相平分,∴![]() =﹣1,解得m=2,又M点在抛物线上,∴y=
=﹣1,解得m=2,又M点在抛物线上,∴y=![]() ×22+
×22+![]() ×2=16,∴M(2,16);
×2=16,∴M(2,16);
②当EM为对角线,即四边形ECMN是平行四边形时,则线段EM的中点横坐标为![]() ,线段CN中点横坐标为﹣3,∵EM,CN互相平分,∴
,线段CN中点横坐标为﹣3,∵EM,CN互相平分,∴![]() =﹣3,解得m=﹣6,又∵M点在抛物线上,
=﹣3,解得m=﹣6,又∵M点在抛物线上,
∴y=![]() ×(﹣6)2+
×(﹣6)2+![]() ×(﹣6)=16,∴M(﹣6,16);
×(﹣6)=16,∴M(﹣6,16);
③当CE为对角线,即四边形EMCN是平行四边形时,则M为抛物线的顶点,即M(﹣2,﹣![]() ).
).
综上可知,存在满足条件的点M,其坐标为(2,16)或(﹣6,16)或(﹣2,﹣![]() ).
).


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,将点P(3,-2)向下平移4个单位长度,得到点P的坐标为( )
A. (-1,-2) B. (3,-6) C. (7,-2) D. (3,-2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子中装有4个除颜色外完全相同的小球,其中黄球1个,红球1个,白球2个,“从中任意摸出2个球,它们的颜色相同”这一事件是事件.(填“随机”或者“确定”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设 A(﹣2,y1),B(1,y2),C(2,y3)是抛物线 y=(x﹣1)2﹣3上的三点,则 y1,y2,y3 的大小关系为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
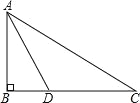
【题目】如图所示,某中学九年级数学兴趣小组测量校内旗杆AB的高度,在C点测得旗杆顶端A的仰角∠BCA=30°,向前走了20米到达D点,在D点测得旗杆顶端A的仰角∠BDA=60°,求旗杆AB的高度.(结果精确到0.1)参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732.
≈1.732.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com