
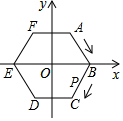
 如图,在平面直角坐标系中,六边形ABCDEF是半径为1的正六边形,点O为正六边形ABCDEF的中心,点P从点B出发,沿正六边形按顺时针方向运动,速度为每秒1个单位长度,则第2017秒时,点P的坐标是( )
如图,在平面直角坐标系中,六边形ABCDEF是半径为1的正六边形,点O为正六边形ABCDEF的中心,点P从点B出发,沿正六边形按顺时针方向运动,速度为每秒1个单位长度,则第2017秒时,点P的坐标是( )| A. | ($\frac{1}{2}$,-$\frac{\sqrt{3}}{2}$) | B. | (-1,0) | C. | (-$\frac{1}{2}$,-$\frac{\sqrt{3}}{2}$) | D. | ($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$) |
分析 由于2017=6×336+1,则可判断第2017秒时,点P运动到点C,作CH⊥x轴于H,如图,根据正六边形的性质得到OB=BC=1,∠BCD=120°,所以∠BCH=30°,再通过解直角三角形求出CH和BH,然后写出C点坐标即可.
解答 解:∵2017=6×336+1,
∴第2017秒时,点P运动到点C,
作CH⊥x轴于H,如图,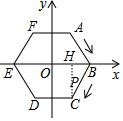
∵六边形ABCDEF是半径为1的正六边形,
∴OB=BC=1,∠BCD=120°,
∴∠BCH=30°,
在Rt△BCH中,BH=$\frac{1}{2}$BC=$\frac{1}{2}$,CH=$\sqrt{3}$BH=$\frac{\sqrt{3}}{2}$,
∴OH=OB-BH=$\frac{1}{2}$,
∴C点坐标为($\frac{1}{2}$,-$\frac{\sqrt{3}}{2}$),
∴第2017秒时,点P的坐标是($\frac{1}{2}$,-$\frac{\sqrt{3}}{2}$).
故选A.
点评 本题考查了规律型:点的坐标:利用正多边形的性质确定动点的运动规律.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
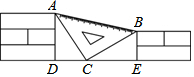 课间,小聪拿着老师的等腰直角三角板玩,不小心掉到两墙之间(如图),∠ACB=90°,AC=BC,从三角板的刻度可知AB=20cm,小聪很快就知道了砌墙砖块的厚度的平方(每块砖的厚度相等)为$\frac{200}{13}$cm.
课间,小聪拿着老师的等腰直角三角板玩,不小心掉到两墙之间(如图),∠ACB=90°,AC=BC,从三角板的刻度可知AB=20cm,小聪很快就知道了砌墙砖块的厚度的平方(每块砖的厚度相等)为$\frac{200}{13}$cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
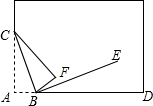 如图,将长方形纸片的一角折叠,使顶点A落在F处,折痕为BC.
如图,将长方形纸片的一角折叠,使顶点A落在F处,折痕为BC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
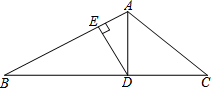 如图,AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,AB=8,DE=4,AC=6,则△ACD的面积为( )
如图,AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,AB=8,DE=4,AC=6,则△ACD的面积为( )| A. | 8 | B. | 10 | C. | 12 | D. | 24 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
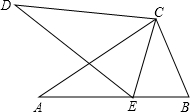 如图,△ABC≌△DEC,点B的对应点E在线段AB上,若AB∥CD,∠D=32°,则∠B的度数是( )
如图,△ABC≌△DEC,点B的对应点E在线段AB上,若AB∥CD,∠D=32°,则∠B的度数是( )| A. | 56° | B. | 68° | C. | 74° | D. | 75° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{5}{2}$ x2y与-$\frac{3}{2}$ xy3 | B. | -8a2b与5a2c | C. | $\frac{1}{4}$ pq与-$\frac{5}{2}$ qp | D. | 19abc与-28ab |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com