
如图,AB是⊙O的弦,OP⊥OA交AB于点P,过点B的直线交OP的延长线于点C,且CP=CB.
(1)求证:BC是⊙O的切线;
(2)若⊙O的半径为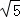 ,OP=1,求BC的长.
,OP=1,求BC的长.

 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案科目:初中数学 来源: 题型:
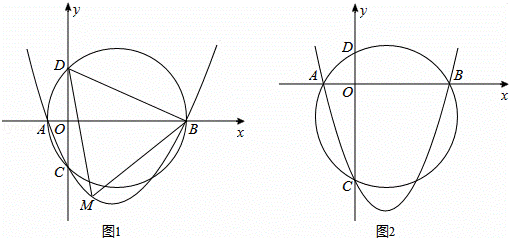
如图,已知抛物线y=ax2+bx+c(a>0,c<0)交x轴于点A,B,交y轴于点C,设过点A,B,C三点的圆与y轴的另一个交点为D.
(1)如图1,已知点A,B,C的坐标分别为(﹣2,0),(8,0),(0,﹣4);
①求此抛物线的表达式与点D的坐标;
②若点M为抛物线上的一动点,且位于第四象限,求△BDM面积的最大值;
(2)如图2,若a=1,求证:无论b,c取何值,点D均为顶点,求出该定点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
若点A(2,4)在函数y=kx的图象上,则下列各点在此函数图象上的是( )
|
| A. | (1,2) | B. | (﹣2,﹣1) | C. | (﹣1,2) | D. | (2,﹣4) |
查看答案和解析>>
科目:初中数学 来源: 题型:
在一个不透明的布袋里装有4个标有1,2,3,4的小球,它们的形状、大小、质地完全相同,小李从布袋里随机取出一个小球,记下数字为x,小张在剩下的3个小球中随机取出一个小球,记下数字为y,这样确定了点Q的坐标(x,y).
(1)画树状图或列表,写出点Q所有可能的坐标;
(2)求点Q(x,y)在函数y=﹣x+5图象上的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com