
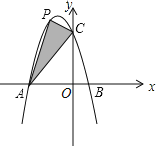
【题目】在平面直角坐标系xOy中,抛物线![]() 与x轴交于
与x轴交于![]() ,点
,点![]() 两点,与y轴交于点C
两点,与y轴交于点C
![]() 求抛物线的解析式:
求抛物线的解析式:
![]() 若点P是抛物线上在第二象限内的一个动点,且点P的横坐标为t,连接PA、PC、AC.
若点P是抛物线上在第二象限内的一个动点,且点P的横坐标为t,连接PA、PC、AC.
![]() 求
求![]() 的面积S关于t的函数关系式.
的面积S关于t的函数关系式.
![]() 求
求![]() 的面积的最大值,并求出此时点P的坐标.
的面积的最大值,并求出此时点P的坐标.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a,b,c是常数,a≠0)与x轴交于A,B两点,顶点P(m,n).给出下列结论
①2a+c>0;
②若![]() 在抛物线上,则y1>y2>y3
在抛物线上,则y1>y2>y3
③关于x的方程ax2+bx+k=0有实数解,则k>c﹣n;
④当n=﹣![]() 时,△ABP为等腰直角三角形;
时,△ABP为等腰直角三角形;
其中正确结论个数有( )个.
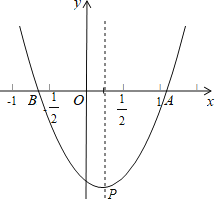
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:![]() 内接于
内接于![]() ,
,![]() ,直径
,直径![]() 交弦
交弦![]() 于点
于点![]() .
.
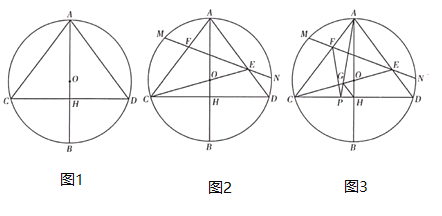
(1)如图1,求证:![]() ;
;
(2)如图2,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,弦
,弦![]() 经过点
经过点![]() ,交
,交![]() 于点
于点![]() ,若
,若![]() ,求证:
,求证:![]() ;
;
(3)如图3,在(2)的条件下,点![]() 为线段
为线段![]() 上一点,连接
上一点,连接![]() ,
,![]() ,
,![]() ,
,![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上.将△ABC绕点A顺时针旋转90°得到△AB1C1.
(1)在网格中画出△AB1C1;
(2)计算点B旋转到B1的过程中所经过的路径长.(结果保留π)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把![]() 置于平面直角坐标系中,点A的坐标为
置于平面直角坐标系中,点A的坐标为![]() ,点B的坐标为
,点B的坐标为![]() ,点P是
,点P是![]() 内切圆的圆心,将
内切圆的圆心,将![]() 沿x轴的正方向作无滑动滚动,使它的三边依次与x轴重合。第一次滚动后,圆心为
沿x轴的正方向作无滑动滚动,使它的三边依次与x轴重合。第一次滚动后,圆心为![]() ,第二次滚动后圆心为
,第二次滚动后圆心为![]() …依次规律,第2019次滚动后,
…依次规律,第2019次滚动后,![]() 内切圆的圆心
内切圆的圆心![]() 的坐标是( )
的坐标是( )
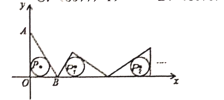
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某游乐园有一个直径为16米的圆形喷水池,喷水池的周边有一圈喷水头,喷出的水柱为抛物线,在距水池中心3米处达到最高,高度为5米,且各方向喷出的水柱恰好在喷水池中心的装饰物处回合,如图所示,以水平方向为![]() 轴,喷水池中心为原点建立平面直角坐标系.
轴,喷水池中心为原点建立平面直角坐标系.
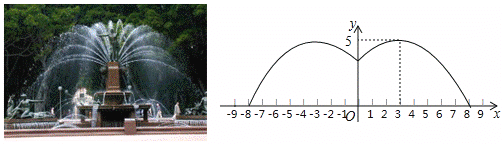
(1)求水柱所在抛物线(第一象限部分)的函数表达式;
(2)王师傅在喷水池内维修设备期间,喷水管意外喷水,为了不被淋湿,身高1.8米的王师傅站立时必须在离水池中心多少米以内?
查看答案和解析>>
科目:初中数学 来源: 题型:
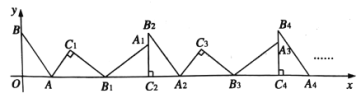
【题目】如图,在平面直角坐标系中,将![]() 绕点
绕点![]() 顺时针旋转到
顺时针旋转到![]() 的位置,点
的位置,点![]() 、
、![]() 分别落在点
分别落在点![]() 、
、![]() 处,点
处,点![]() 在
在![]() 轴上,再将
轴上,再将![]() 绕点
绕点![]() 顺时针旋转到
顺时针旋转到![]() 的位置,点
的位置,点![]() 在
在![]() 轴上,将
轴上,将![]() 绕点
绕点![]() 顺时针旋转到
顺时针旋转到![]() 的位置,点
的位置,点![]() 在
在![]() 轴上,依次(无滑动)进行下去…….若点
轴上,依次(无滑动)进行下去…….若点![]() 、
、![]() ,则点
,则点![]() 的坐标为______.
的坐标为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
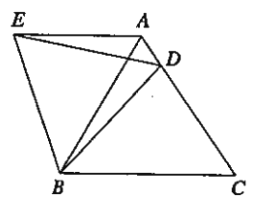
【题目】在等边 ![]() 中,
中,![]() 是边
是边 ![]() 上一点,连接
上一点,连接 ![]() ,将
,将 ![]() 绕点
绕点 ![]() 逆时针旋转
逆时针旋转 ![]() ,得到
,得到 ![]() ,连接
,连接 ![]() ,若
,若 ![]() ,
,![]() ,有下列结论:①
,有下列结论:① ![]() ;②
;② ![]() ;③
;③ ![]() 是等边三角形;④
是等边三角形;④ ![]() 的周长是
的周长是 ![]() .其中,正确结论的个数是
.其中,正确结论的个数是 ![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边由长为30米的篱笆围成.已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边长为x米.
(1)若苗圃园的面积为72平方米,求x;
(2)若平行于墙的一边长不小于8米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值;如果没有,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com