
����Ŀ��ijУΪ��ʵ��������������Ϣ��2.0�ж��ƻ���������ֻ�Уƽ̨����Ҫ����һ�����Ӱװ��ƽ����ԣ�������2̨���Ӱװ��6̨ƽ����Թ���9��Ԫ������3̨���Ӱװ��4̨ƽ����Թ���11��Ԫ��
��1������Ӱװ��ƽ����Եĵ��۸��Ƕ�����Ԫ��
��2�����ѧУʵ�ʣ���У��������Ӱװ��ƽ����Թ�100̨�����е��Ӱװ����ٹ���6̨�Ҳ�����24̨��ij�̼Ҹ����������Żݷ���������һ�����Ӱװ��ƽ����Ծ�����ۣ�����������1̨���Ӱװ壬��1̨ƽ����ԣ���������Ӱװ�a��̨������ķ���ΪW����Ԫ��������������Żݷ����ֱ�д��W����a�ĺ�����ϵʽ����������УӦѡ�������Żݷ��������ʡǮ��
���𰸡���1�����Ӱװ�ĵ�����3��Ԫ��ƽ����Եĵ�����0.5��Ԫ������2������һ��W����a�ĺ�����ϵʽ��W��2.25a+45����������W����a�ĺ�����ϵʽ��W��2a+50����6��a��20ʱ������һ��ʡǮ����a��20ʱ�����ַ�������һ������20��x��24ʱ����������ʡǮ��
��������
��1���������⣬�г���Ӧ�Ķ�Ԫһ�η����飬�Ӷ�������õ��Ӱװ��ƽ����Եĵ��۸��Ƕ�����Ԫ��
��2���������⣬�ֱ�д�����ַ����£�W����a�ĺ�����ϵʽ�������÷������۵ķ������Եõ���УӦѡ�������Żݷ��������ʡǮ��
�⣺��1���蹺����Ӱװ�ĵ���Ϊx��Ԫ��ƽ����Եĵ�����y��Ԫ��
![]() ��
��
��ã� ![]() ��
��
�𣺵��Ӱװ�ĵ�����3��Ԫ��ƽ����Եĵ�����0.5��Ԫ����
��2��������ɵã�
����һ��W��[3a+0.5��100��a��]��0.9��2.25a+45��
��������W��3a+0.5��100��a��a����2a+50��
��2.25a+45��2a+50ʱ����a��20��
����6��a��20ʱ��ѡ��һ��
��2.25a+45��2a+50ʱ����a��20��
����a��20ʱ������һ�ͷ���������һ���ࣻ
��2.25a+45��2a+50����a��20��
����20��x��24ʱ��ѡ������
�𣺷���һ��W����a�ĺ�����ϵʽ��W��2.25a+45����������W����a�ĺ�����ϵʽ��W��2a+50����6��a��20ʱ������һ��ʡǮ����a��20ʱ�����ַ�������һ������20��x��24ʱ����������ʡǮ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��ά��������Ȩ�ͺ���Ȩ�������ಿ�Ŷ��ҹ��캣ʵ���˳�̬��Ѳ����������ͼ������ִ��Ѳ������ĺ��ബ��ÿСʱ50������ٶ������������У���![]() ����õ���
����õ���![]() �ڱ�ƫ��
�ڱ�ƫ��![]() �����ϣ���������1Сʱ����
�����ϣ���������1Сʱ����![]() ������ʱ��õ���
������ʱ��õ���![]() �ڱ�ƫ��
�ڱ�ƫ��![]() �����ϣ�
�����ϣ�
��1����![]() �Ķ�����
�Ķ�����
��2����֪�ڵ���![]() ����Χ25�������а������ʺ��ബ�����������������Ƿ�ȫ��
����Χ25�������а������ʺ��ബ�����������������Ƿ�ȫ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У���A=90������D���߶�BC�ϣ���EDB=![]() ��C��BE��DE������ΪE��DE��AB�ཻ�ڵ�F��
��C��BE��DE������ΪE��DE��AB�ཻ�ڵ�F��
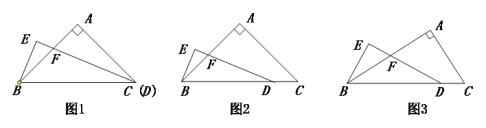
̽������AB=AC��C��D�����غ�ʱ����ͼ1��̽����
��1���߶�BE��FD֮���������ϵ��ֱ��д����� ��
��2����EBF= ��
֤������AB=AC��C��D���غ�ʱ��̽���߶�BE��FD��������ϵ��������֤����
���㣺��AB=![]() ACʱ����ͼ����
ACʱ����ͼ����![]() ��ֵ ���ú�
��ֵ ���ú�![]() ��ʽ�ӱ�ʾ����
��ʽ�ӱ�ʾ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���y=x+4��ͼ���뷴��������y=![]() ��kΪ������k��0����ͼ����A����1��a����B���㣬��x�ύ�ڵ�C��
��kΪ������k��0����ͼ����A����1��a����B���㣬��x�ύ�ڵ�C��
��1����˷����������ı���ʽ��
��2������P��x���ϣ���S��ACP=![]() S��BOC�����P�����꣮
S��BOC�����P�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD����O���ڽ��ı��Σ�BC����O��ֱ����OE��BC��AB�ڵ�E����BE=2AE������ADC =_________����
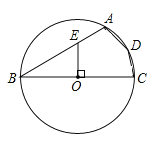
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������![]() ��
��![]() ����E��
����E��![]() �ϣ���Ϊ
�ϣ���Ϊ![]() ���е㣬��
���е㣬��![]() ���߶�
���߶�![]() �ķ���͢�����ϣ��������̶ȵ�ֱ�߰�����Ҫ��ͼ��������ͼ�ĺۼ�����
�ķ���͢�����ϣ��������̶ȵ�ֱ�߰�����Ҫ��ͼ��������ͼ�ĺۼ�����
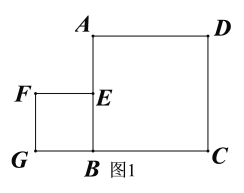
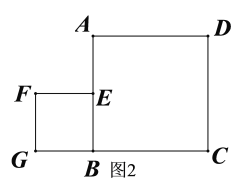
��1����ͼ1�У�����![]() ���е�
���е�![]() ��
��
��2����ͼ2�У�����![]() �Ĵ�ֱƽ���ߣ�
�Ĵ�ֱƽ���ߣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ���������������Ĺ�������ͼ�����ݸ�����ͼ������˵����
�������ֵyΪ![]() ʱ������ֵxΪ3��9��
ʱ������ֵxΪ3��9��
��������ֵxΪ16ʱ�����ֵyΪ![]() ��
��
�������������������y��������������x��ʹ������x���ܹ����y��
������������������x������x֮���������ܹ�һֱ���У���ʼ�ղ������yֵ�����д�����ǣ�������
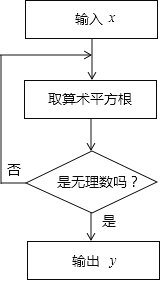
A.�٢�B.�ڢ�C.�٢�D.�٢�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����OABC�Ķ���A��C�ֱ���x��y����������ϣ�����B������Ϊ��4��2����M�DZ�BC�ϵ�һ�����㣨����B��C�غϣ�������������![]() ��k��0��x��0����ͼ����M�����AB���ڵ�N������MN��
��k��0��x��0����ͼ����M�����AB���ڵ�N������MN��
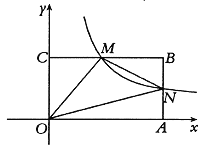
��1������M�DZ�BC���е�ʱ�����������ı���ʽ��
��2���ڵ�M���˶������У���֤����![]() ��һ����ֵ��
��һ����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У�
��![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() ��
��![]() �Ľ�ƽ�����ཻ�ڵ�
�Ľ�ƽ�����ཻ�ڵ�![]() ��
��![]() ��
Ϊ��![]() ���е㣬
���е㣬![]() ����
����![]() �� ��
�� ��

A.125��B.145��C.175��D.190��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com